
Prostředí:

Prostředí:
Šiframi k porozumění desítkové soustavě.
Algebrogramy budují porozumění desítkové soustavě a umožňují odhalovat hlubší souvislosti aritmetiky. Rozvíjejí i kombinatorické myšlení a schopnost argumentace. Algebrogramy patří mezi nejnáročnější úlohy, se kterými se žák na 1. stupni setká. Připomínají šifry.
Když ve vztahu 26 + 6 = 32 zašifrujeme číslice 2 a 6 písmeny A a B, dostaneme algebrogram AB +B = 32. Za stejná písmena dosazujeme stejné číslice, za různá písmena různé číslice.První číslice dvojmístného a vícemístného čísla nesmí být nula.
Vyřešit algebrogram znamená najít číslice, které se za písmeny skrývají, a najít všechna řešení. Náš algebrogram má dvě řešení AB = 26 a AB = 31, neboť i 31 + 1 = 32. Hledání řešení vede k mnohým výpočtům, které žáci nepociťují jako nudu. Algebrogramy lze řešit metodou pokus-omyl, protože každé písmeno může nabývat nejvýš deseti hodnot: 0, 1… 9.
Hvězdičkogramy používají k označení číslic pouze hvězdičky. Například, když máme vrátit neposedy 3, 5 a 6 do výpočtu ** · * = 210, budeme zkoušet 56 · 3, nebo 63 · 5, nebo 35 · 6. Poslední pokus se zdařil, máme výsledek.
Většina úloh je gradovaná. To značí, že obsahuje podúlohy a), b), c), … s rostoucí náročností. To umožní každému dítěti najít si přiměřenou úlohu. Nejlehčí jsou algebrogramy, ve kterých je jen jedno písmeno.
Úloha 1: Vyřeš algebrogramy:
a) AA = 30 + A,
b) BB = 50 + B,
c) CC + C = 24,
d) DD + D + D = 65,
e) EE + E + E = 39,
f) A · A = A + A,
g) B · B = B + B + B,
h) C · C = C + C + C + C
Úloha 2: Vyřeš algebrogramy. Najdi všechna řešení:
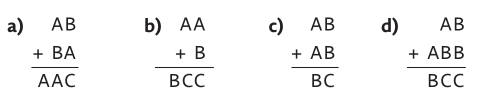
Úloha 3: Vyřeš algebrogramy. Najdi všechna řešení:
a) A · A = B,
b) C · C = D + D,
c) E · E + E = DD – D
Úloha 4: Vyřeš algebrogramy na dělení se zbytkem:
a) AA : 2 = B(A),
b) AA : 4 = B(A),
c) AA : 5 = B(A),
d) AA : 6 = B(A),
e) AA : 8 = B(A)
Úloha 1:
a) A = 3;
b) B = 5;
c) C = 2;
d) D = 5;
e) E = 3;
f) A = 2;
g) B = 3;
h) C = 4.
Úloha 2:
a) A = 1, B = 9, C = 0;
b) A = 9, B = 1, C = 0;
c) pět řešení: A = 1, B = 2, C = 4; A = 2, B = 4, C = 8; A = 2, B = 5, C = 0; A = 4, B = 9, C = 8; A = 3, B = 7, C = 4
d) čtyři řešení: A = 4, B = 5, C = 0; A = 5, B = 6, C = 2; A = 6, B = 7, C = 4; A = 7, B = 8, C = 6.
Úloha 3:
a) dvě řešení A = 2, B = 4; A = 3, B = 9;
b) C = 4, D = 8;
c) dvě řešení E = 4, D = 2; E = 5, D = 3.
Úloha 4:
a) A = 1, B = 5;
b) A = 2, B = 5;
c) čtyři řešení A = 1, B = 2; A = 2, B = 4; A = 3, B = 6; A = 4, B = 8;
d) A = 3, B = 5; e) A = 4, B = 5.
Objevují se úlohy zaměřené na mocniny, rovnice, výrazy, dělitelnost, racionální čísla.
Úloha 5: Vyřeš algebrogramy:
a) A · A · A = B,
b) A · A · A = B · B,
c) A · A · A = A · B,
d) ABC = C · C · C,
e) ABA = C · C · C,
f) AB · AB = CAB,
g) AAAB = B · B · B · B · B
Úloha 6: Vyřeš algebrogramy:
a) (A + A + A) : A = A,
b) (BB + B) : B = AB,
c) AB : A = CC(C)
Úloha 7: Vyřeš algebrogram KL + L = 28 v případě, že číslice L je a) sudá, b) lichá.
Úloha 8: Vyřešte algebrogramy:
a) 37 : A = B(2),
b) 37 : C = D(1),
c) 37 : E = F(5),
d) 37 : G = H(7)
Úloha 9: Aleš vyřešil všechny algebrogramy a říká spolužákům: „Vyřešte algebrogram AB : n = B(A) pro každé přirozené číslo n větší než jedna.“ Dokážete to také?
Úloha 10: Řešte hvězdičkogramy, v nichž každá * je nenulová číslice:
a) 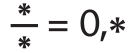 Najděte všech 8 řešení.
Najděte všech 8 řešení.
b) 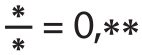 Najděte všechna 4 řešení.
Najděte všechna 4 řešení.
Úloha 5:
a) A = 2, B = 8;
b) A = 4, B = 8;
c) dvě řešení A = 2, B = 4; A = 3, B = 9;
d) tři řešení A = 1, B = 2, C = 5; A = 2, B = 1, C = 6; A = 7, B = 2, C = 9;
e) A = 3, B = 4, C = 7;
f) A = 2, B = 5, C =6;
g) A = 7, B = 6.
Úloha 6:
a) A = 3;
b) A = 1, B = 2;
c) sedm řešení A = 2, B = 3, C = 1; A = 3, B = 4, C = 1; A = 4, B = 5, C = 1; A = 5, B = 6, C = 1; A = 6, B = 7, C = 1; A = 7, B = 8, C = 1; A = 8, B = 9, C = 1.
Úloha 7:
a) K = 2, L = 4;
b) K = 1, L = 9.
Úloha 8:
a) dvě řešení A = 5, B = 7; A = 7, B = 5;
b) dvě řešení C = 4, D = 9; C = 9, D = 4;
c) E = 8, F = 4;
d) nemá řešení.
Úloha 9:
n = 2: A = 1, B = 9; n = 3: A = 2, B = 9; n = 4: tři řešení A = 1, B = 3; A = 2, B = 6; A = 3, B = 9; n = 5: A = 4, B = 9; n = 6: A = 5, B = 9; n = 7: A = 6, B = 9; n = 8: A = 7, B = 9; n = 9: A = 8, B = 9.
Úloha 10:
a) 1/2 = 0,5; 2/4 = 0,5; 3/6 = 0,5; 4/8 = 0,5; 1/5 = 0,2; 2/5 = 0,4; 3/5 = 0,6; 4/5 = 0,8;
b) 1/4 = 0,25; 2/8 = 0,25; 3/4 = 0,75; 6/8 = 0,75.