
Prostředí:

Prostředí:
Manipulativní zkušeností k porozumění 2D geometrii
Představíme nyní prostředí, ve kterém děti získávají mnoho zkušeností s geometrickými útvary, jejich vlastnostmi a vztahy mezi nimi, v němž mají možnost snadno argumentovat a vyvozovat pravidla. Zkušenosti, které procházejí rukama, jsou cenné.
Začneme tedy manipulacemi na geoboardu. Geoboard je deska s 9 (nebo i více) kolíky rozmístěnými do čtverce 3 × 3 (4 × 4, 5 × 5, …). Na kolíky natahujeme barevné gumičky a tvoříme různé obrazce.
S řadou činností, které dále uvedeme pro žáky 1.−2. ročníku, mohou začít i děti v předškolním věku. Důležité je, že dítě zde „myslí rukama“ a poznává pojmy, které později dostanou název jako mnohoúhelník, vrchol, strana, úhlopříčka apod. Začínáme volnou tvorbou. Žáci si s geoboardem hrají, tvoří různé obrazce.
O nich si povídáme. Děti používají metaforický jazyk – vypadá to jako
domeček, jako zobák apod. Dospělý děti neopravuje, ale sám se snaží
používat správné termíny. Ty pak děti od něj postupně převezmou.
K těmto čtyřem obrazcům se budou vztahovat úlohy 1. až 7.
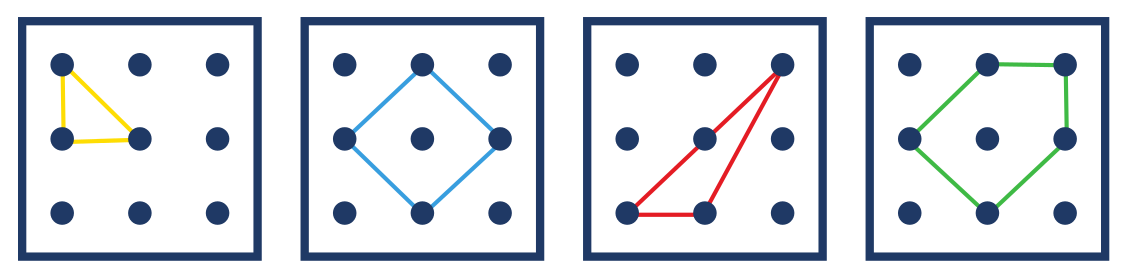
Úloha 1: Vytvoř na svůj geoboard postupně obrazce podle obrázku.
Při kopírování obrazce na geoboard dítě začíná obrazec vnímat hlouběji. Už nestačí, že vypadá jako šipka, ale vnímá jeho vlastnosti, např. má pět vrcholů, různě dlouhé strany, pravý úhel, gumička se dotýká pěti kolíků apod. Dítě při kopírování obrazce analyzuje.
Časté diskuse se týkají druhého modrého obrázku. Je to kosočtverec, nebo čtverec? Dítě vidí čtverec „postavený na koso“. Geoboard ale umožní obrazcem pootočit a žáci tak poznávají, že název obrazce nezáleží na jeho poloze. Vidí, že je to čtverec.

Následující série úloh směruje naši pozornost na pojem délka úsečky a obsah obrazce, jednotka obsahu a odhalení způsobu, jak určit obsah útvaru bez vzorečku.
Úloha 2: Modrý tvar rozděl na dvě stejné části. Totéž udělej se žlutým i zeleným tvarem.
Úloha 3: Ke žlutému trojúhelníku přidej hnědý trojúhelník tak, aby oba trojúhelníky dohromady tvořily čtverec.
Úloha 4: K červenému trojúhelníku přidej hnědý trojúhelník tak, aby oba trojúhelníky dohromady tvořily trojúhelník, který je zvětšením trojúhelníka žlutého (tj. trojúhelník pravoúhlý, rovnoramenný).
Úloha 5: Červený trojúhelník má tři strany a zelený pětiúhelník jich má pět. Uspořádej tyto strany od nejkratší po nejdelší.
Úloha 6: Představ si, že máš trojúhelníkový kachlík, který se přesně vejde do žlutého trojúhelníka. Kolik takových kachlíků je třeba na pokrytí a) modrého čtverce, b) zeleného pětiúhelníku?
Úloha 2: Modrý čtverec lze rozdělit na dvě shodné části mnoha způsoby. Na první čtyři děti z 1.–2. ročníku přijdou, na další dva i mnohé neuvedené přijdou až později, možná až na druhém stupni.

Úloha 3:
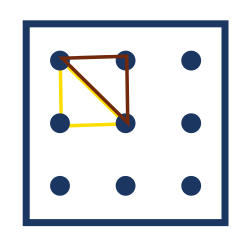
Úloha 4:
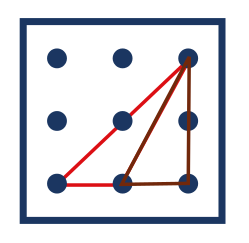
Úloha 6:
a) 4r;
b) 5r.
Z geoboardu přecházíme na čtvercovou mříž. Z kolíků se staly mřížové body a obrazcům budeme říkat mřížové – mřížový trojúhelník atd. Při hře Telefon děti popisují mřížové obrazce jakoby někomu do telefonu. Pak dostanou výzvu, aby zapsaly obrazce pomocí znaků. Po několika pokusech a diskusích se objeví šipkový zápis mřížového obrazce, neboť jazyk šipek znají děti z Krokování.
Na obrázku je trojúhelník KLM, který je zapsán pomocí šipek takto:
K →→↑ L ↑← M ←↓↓ K.
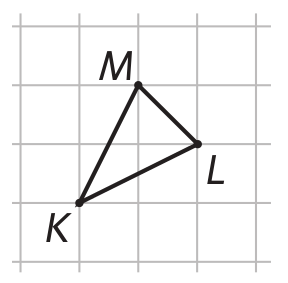
Zápis čteme: Začínám v bodě K, udělám dva kroky vpravo, jeden nahoru a zde označím bod L. Z bodu L pokračuji krok nahoru, krok doleva a zde je bod M. Pro kontrolu z M udělám jeden krok doleva a dva dolů, jsem opět v K. Narýsuji úsečku KL, LM a také MK.
Úloha 7: Tři šipkové zápisy popisují tři obrazce z obrázku nad první úlohou. Vrcholy nejsou popsány písmeny, pouze označeny tečkami. Najdi je a doplň šipkový zápis čtvrtého obrazce.

Úloha 8: Zjisti obsah žlutého, modrého i červeného trojúhelníku na obrázku. Žáci snadno zjistí, že modrý trojúhelník má obsah 2 kachlíky, protože je to polovina celého čtverce a ten má obsah 4 kachlíky. Žlutý trojúhelník je polovina obdélníku s obsahem 2 kachlíky, tedy má obsah 1 kachlík.

Pak některý žák objeví klíčovou myšlenku: červený trojúhelník získáme, když od čtverce (4 kachlíky) „odřízneme“ modrý a žlutý trojúhelník.
Tedy pro výpočet obsahu platí:  . Obsah červeného trojúhelníku je jeden kachlík.
. Obsah červeného trojúhelníku je jeden kachlík.
Úloha 7: Šipkové zápisy jsou zápisy těchto obrazců: pětiúhelník, červený trojúhelník, žlutý trojúhelník. Chybějící zápis čtverce je 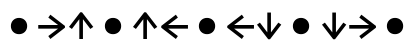
Úloha 8: Žlutý trojúhelník, S = 1/2  ; modrý čtverec, S = 2
; modrý čtverec, S = 2  ; červený trojúhelník, S = 1
; červený trojúhelník, S = 1 
Následující úlohy jsou přípravou na objev Pythagorovy věty.
Úloha 10: Je dána úsečka AB šipkovým zápisem
a) A →↑ B
b) A →→↑ B
c) A →→→↑ B
d) A →…→↑ B (tři tečky znamenají, že šipek doprava bude libovolně)
Nakresli ji v mříži a dorýsuj čtverec ABCD.
Dopiš šipkový zápis čtverce a spočítej jeho obsah.
Úloha 10:
a) A →↑ B ↑← C ←↓ D ↓→ A; 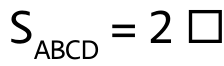 ; (A ↑→ B →↓ C ↓← D ←↑ A)
; (A ↑→ B →↓ C ↓← D ←↑ A)
b) A →→↑ B ↑↑← C ←←↓ D ↓↓→ A; 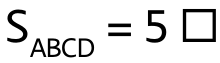 ; (A ↑→→ B →↓↓ C ↓←← D ←↑↑ A)
; (A ↑→→ B →↓↓ C ↓←← D ←↑↑ A)
c) A →→→↑ B ↑↑↑← C ←←←↓ D ↓↓↓→ A; 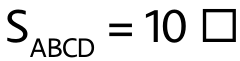 ; (A ↑→→→ B →↓↓↓ C ↓←←← D ←↑↑↑ A)
; (A ↑→→→ B →↓↓↓ C ↓←←← D ←↑↑↑ A)
d) V zápise znamenají tři tečky, že šipek doprava bude libovolně. To můžeme zapsat pomocí n, což znamená jakékoliv přirozené číslo. Obrázek již nakreslit neumíme, ale šipkový zápis zapsat umíme. n šipek doprava zapíšeme takto 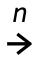 . Obdobně zapíšeme n šipek nahoru, doleva a dolů.
. Obdobně zapíšeme n šipek nahoru, doleva a dolů.