
Prostředí:

Prostředí:
Tabulky, grafy, statistika i náhoda
Už když dítě hraje běžné hry jako Pexeso nebo Černého Petra, učí se porovnávat, přiřazovat a třídit. Když potom třídí hračky podle nějakých pravidel, zlepšuje schopnost organizovat soubor dat.
Na obrázku vidíme pomůcku Pavly Polechové – sadu jednobarevných obrázků zvířátek. Dítě ukládá obrázky a tvoří různé vzory. Například dá k sobě všechny červené nebo všechny pejsky. Nebo dá k sobě pejska a kočičku. Nebo zelenými zvířátky vyplní celý řádek a pejsky celý sloupec. Tak objeví důležité dvojrozměrné uspořádání: v jednom směru stejné barvy, ve druhém stejná zvířátka.

Dítě, které rádo hraje stolní hry, například Člověče, nezlob se, můžeme motivovat otázkou: „Které číslo padá nejčastěji?“ Prozkoumáme to experimentem. Na papír napíšeme čísla od 1 do 6; dítě hodí kostkou, padne třeba 4, a tak na číslo 4 položí dítě jedno víčko. V dalším hodu padne třeba 1 a dítě položí další víčko na číslo 1. Po 10 hodech bude například na čísle 5 sloupec tří víček, ale na čísle 6 nebude ani jedno. Tak vzniká první histogram. Když ale během dvou dnů uděláme sto hodů, začnou se sloupce vyrovnávat. Dítě získává první zkušenost s pravděpodobností.
Tabulky jsou v běžném životě všude kolem nás. V prostředí Autobus (viz 2. díl) děti tabulku objeví. Přijdou na to, že je to velmi efektivní způsob zápisu. Už od 1. ročníku tak děti vytváří tabulky a zjišťují z nich odpovědi na různé otázky.
Úloha 1: Do tabulky zapiš, kolik je čeho.
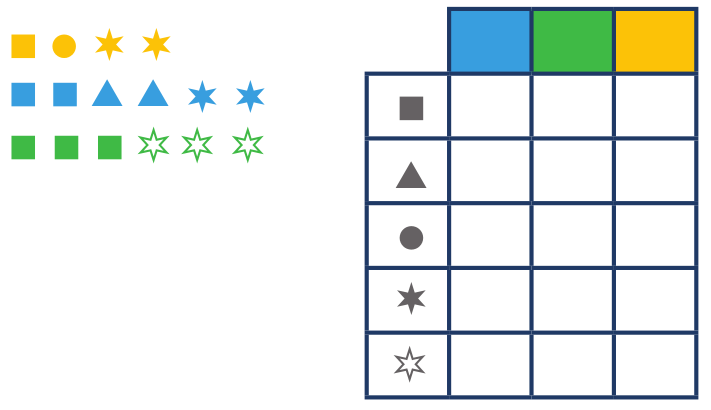
K úloze pokládáme doplňující otázky jako například: Kolik je na obrázku všech zelených symbolů? Kolik čtverečků? Kolik modrých hvězdiček? Některé dítě zde počítá symboly. To dítě, které k odpovědím použije tabulku, dokáže již tento nástroj záznamu využívat.
Oblíbená je hra na Sovu. Je dána galerie objektů. Například jména: Adam, Anna, Emil, Eva. Sova (jeden ze žáků) na jedno jméno myslí. Spolužáci mají jméno uhodnout. Na jejich otázky Sova odpovídá jen ANO, nebo NE. Počet jmen může být výrazně větší. Místo jmen mohou být například písmena, obrázky nebo čísla.
Úloha 2: Sova myslí na jedno z čísel 2, 6, 7, 9,12, 13, 14, 15. Spolužáci se ptají, Sova odpovídá. Je dvouciferné? NE. Je sudé? ANO. Je menší než 3? NE. Je větší než 5? ANO.
a) Na které číslo Sova myslí?
b) Která otázka byla zbytečná?
Při hře Sova se děti mimo jiné učí i formulovat otázky, používat přesné termíny a vzájemně si naslouchat.
Úloha 2:
a) Sova myslí na číslo 6.
b) Poslední 4. otázka je zbytečná. Bylo by možné za zbytečnou označit 3. otázku místo 4., protože odpovědi na 1., 2. a 4. otázku též jednoznačně vedou k číslu 6.
Zkoumání náhody, které jsme dělali na úrovni MŠ, uděláme tentokráte se dvěma hracími kostkami.
Úloha 3: Házej dvěma kostkami. Do tabulky zapiš, kolikrát padne součet 2, 3,..., 12. Jaký součet je nejčastější? Proč?
Když třída udělá přes dvě stě hodů, žáci vidí, že nejčastější je součet 7 a součty 2 a 12 padnou jen výjimečně. Vidí, že tabulka je „symetrická“.
O vysvětlení těchto jevů se pokusí především špičkoví žáci. Argumentují tím, že číslo 2 získáme jediným způsobem jako 1 + 1, ale číslo 7 můžeme získat až 6 způsoby: 1 + 6, 2 + 5, 3 + 4, 4 + 3, 5 + 2, 6 + 1. Námitka, že 3 + 4 a 4 + 3 je vlastně jen jedna možnost, vyvolá plodnou diskuzi. Učitel do ní nezasáhne. Žáci sami po jisté době námitku vyvrátí.
Důležitá schopnost pro život je číst grafy.
Úloha 4: Ve škole máme tři 3. třídy a tři 4. třídy.
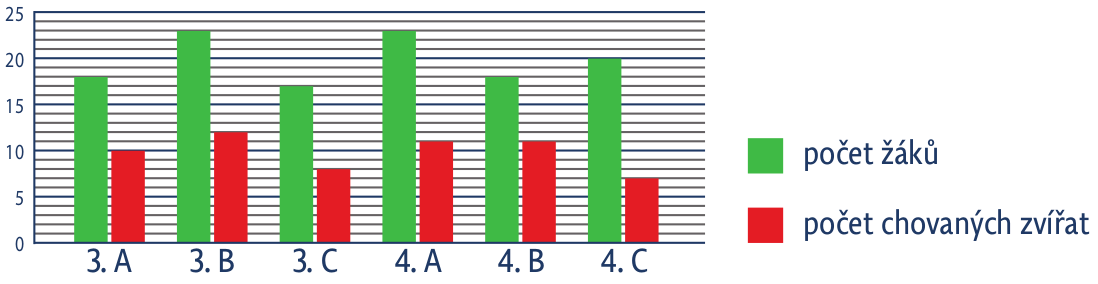
U každé třídy známe počet žáků (zelený sloupec) i počet zvířat, která žáci této třídy chovají (červený sloupec). Odpověz na tyto otázky:
a) Je více žáků ve 3. třídách nebo ve 4. třídách?
b) Jsou 3. třídy více chovatelské než 4. třídy?
c) Která třída je nejméně a která nejvíce chovatelská?
Na této úloze je zřetelná gradace. Zatímco v otázce a) žáci zjišťují informaci, která je z grafu snadno čitelná, otázky b) a c) jsou náročnější. Třída začne diskutovat, co znamená „více chovatelský“. Většinou se jako první objeví názor, že třídy 3. C a 4. C jsou nejméně chovatelské, protože chovají nejméně zvířat. Potom ale přijde žák, který řekne, že 4. C je méně chovatelská, protože má více žáků. Tento žák cítí, že jde o poměr chovaných zvířat ku počtu žáků. K této náročné myšlence otázky b) a c) směřují.
Úloha 3: Námitku, že 3 + 4 a 4 + 3 jsou stejné součty, mohou žáci vyvrátit například tím, že součet 2 padá mnohem výjimečněji než součet 3. Součet 3 totiž dostaneme jako 1 + 2 nebo 2 + 1. Kdybychom 1 + 2 a 2 + 1 považovali za jednu možnost, padal by součet 3 stejně často jako součet 2.
Úloha 4:
a) Ve 3. třídách je 18 + 23 + 17 žáků, což je méně než 23 + 18 + 20.
b) 3. třídy chovají 10 + 12 + 8 zvířat, což je méně než 4. třídy (11 + 11 + 7). Tedy 3. třídy mají méně žáků a více chovaných zvířat, dá se říct, že jsou více chovatelské.
c) Nejméně chovatelská je 4. C, což je jediná třída, ve které je poměr počet zvířat : počet žáků menší než 1 : 2, přesně 7 : 20. Nejvíce chovatelská je 4. B s poměrem 11 : 18.
Statistické zpracování dat je obohaceno o aritmetický průměr. Žáci počítají průměrné známky své i celé třídy. Průměru se ale dotýká například i následující méně tradiční úloha.
Úloha 5: Aneta porovnávala délku ženských a mužských jmen. Z kalendáře vypsala všech 30 jmen začínajících na A. Zjistila, že v nich je 179 písmen. Skoro přesně 6 písmen na jedno jméno. Ale u ženských jmen je to víc než 6 písmen na jméno a u mužských je to méně než 6 písmen na jméno. Aneta tvrdila: „Tedy ženská jména jsou delší.“ Má Aneta pravdu? Tvrzení Anety je záměrně mírně nejasné, protože cílem úlohy je rozproudit ve třídě diskuzi. Mluví Aneta o všech jménech? Co když u jmen začínajících na B to bude naopak? Je možné Anetino tvrzení zpřesnit?
Schopnost porozumět tabulkám, grafům a různým schématům dále rozvíjíme pomocí vývojových diagramů. To jsou v podstatě jednoduché „programy“ a žáci se díky nim učí rozumět principům, jak fungují počítače.
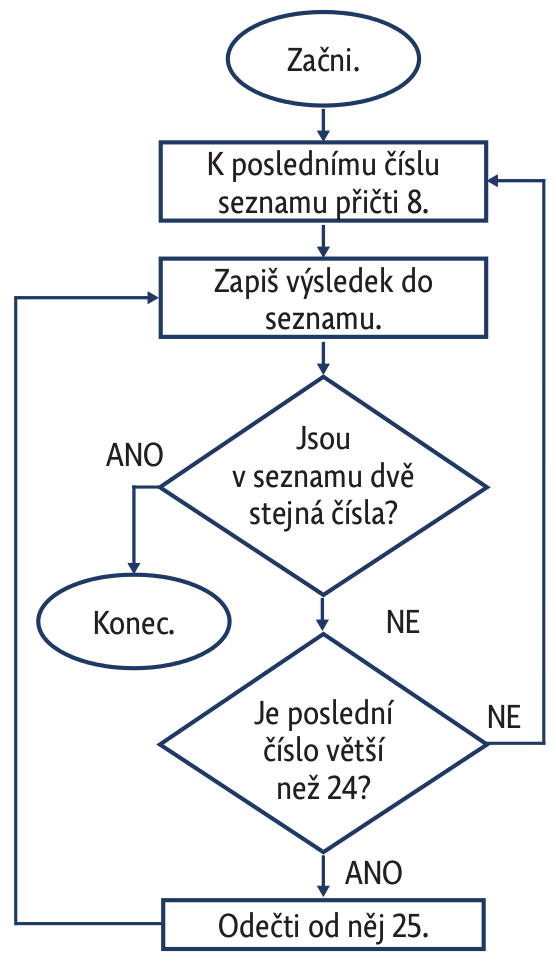
Úloha 6: Budeš vytvářet seznam čísel. Na začátek seznamu si napiš číslo 7 a dále postupuj podle vývojového diagramu.
Úloha 5: Anetino tvrzení by bylo možné upřesnit například takto: Průměrná délka vypsaných ženských jmen je větší než průměrná délka vypsaných mužských jmen. Takové tvrzení je přesnější, ale též obtížněji srozumitelné.
V hovorovém jazyce často mluvíme nepřesně, protože spoléháme na kontext a volíme mezi přesností a srozumitelností. Diskusními úlohami tohoto typu vedeme děti k citlivosti na nepřesnosti a nuance, kterých v životě zneužívají někteří obchodníci. Na letáku se píše třeba „sleva až 40 %“ a přitom jen jedno zboží je zlevněno o 40 %, zatímco sleva ostatního zboží je mnohem menší. Slůvko „až“ navíc bývá zmenšeno, nebo dokonce vynecháno.
Úloha 6: Podle pokynů vzniká seznam: 7, 15, 23, 31, 6, 14, 22, 30, 5, 13, 21, 29, 4, 12, 20, 28, 3, 11, 19, 27, 2, 10, 18, 26, 1, 9, 17, 25, 0, 8, 16, 24, 32, 7.