
Prostředí:

Prostředí:
Zvládnout slovní úlohy znamená především rozumět jazyku, který běžně používáme. I v období, kdy dítě ještě neumí číst, řeší různé úlohy běžného života, které prožívá s rodičem. V bohaté komunikaci s rodiči dítě poznává i mnoho z matematiky – čísla, tvary, vztahy, různé situace.
Ptám se čtyřletého hocha: „Aleši, kdo je syn tvého táty?“ Hoch se zamyslí, podívá se na tátu a řekne: „Já, jo a Petr.“
Pětiletá Bára pomáhá mamince strojit stůl. Máma ji požádá, aby ubrousky přeložila na poloviny. Dívka chvíli kouká a pak se zeptá: „Tak, nebo takto?“ (na trojúhelník nebo na obdélník). Maminka: „Takhle hezky, na trojúhelníky.“
Na posteli leží medvídek, panenka a bagr. Ptáme se: Kolik je to hraček? Přidám na postel ještě autíčko a míč. Kolik hraček jsem přidal? Kolik hraček je na posteli nyní? Medvídka uklidím do police. Kolik hraček jsem ubral? Kolik hraček je na posteli nyní?
Na talíři jsou 4 jablka. Dvě vidím a ostatní jsou pod ubrouskem. Kolik jablek je ukryto pod ubrouskem? V modré misce jsou dvě fazole, v červené čtyři. Kde je víc? O kolik? Z červené misky přesunu jednu fazoli do modré misky. Kde je víc fazolí nyní?
Neváhejme dítko za každý krok pochválit a tvářit se překvapeně, že úlohu zvládlo.
Podobné aktivity jsou důležité i ve školním věku, v době, kdy se dítě číst teprve učí.
Úloha 1: Kolik krychlí má Ivo? Kolik krychlí má Eva? Ivo má __ krychlí. Eva má __ krychlí. Kolik krychlí mají oba? Dohromady mají __ . Kdo má více? Více má __ .
Snaha ulehčit dítěti práci tím, že mu radíme, jak úlohu řešit a co a jak si zapsat, je kontraproduktivní. Dítě cítí, že je podceňujeme a ubíráme mu autonomii. Nechme zcela na dítěti, jak úlohu vyřeší. Případnou chybu si vyjasní rozhovorem nejlépe s jiným dítětem. Důležité je, že dítě ví, co dělá, a umí si své řešení obhájit. Vítaným a účinným nástrojem řešení slovních úloh je dramatizace – situaci s dítětem sehrajeme, nebo aspoň modelujeme. Vítána je také metoda pokus – omyl, při které dítě získává se situací mnoho zkušeností, jako například v následujících již obtížnějších úlohách.
Úloha 2: Mám komín z pěti krychlí. Postav svůj komín tak, že můj bude o jednu krychli vyšší než ten tvůj.
Často dítě postaví komín ze šesti krychlí. Nechá se zmást slovem vyšší a jednu krychli přidá. Vzájemným porovnáním komínů a diskusí dítě zjistí, že musí lépe poslouchat. První slovní úlohy v učebnici jsou takové, že si dítě potřebné informace vyhledává z obrázku. To přispívá k tomu, že později lépe vyhledává klíčové informace i v psaném textu.
Úloha 3: Goran a Petr mají dohromady 12 Kč. Goran má 2 mince a Petr 3. Přesto má Goran o 2 Kč více než Petr. Které mince má Goran o které Petr?
Úloha 4: Když byly Mirkovi 3 roky, narodily se jeho sestry, dvojčata Dana a Jana. Až bude Mirkovi 5 let, budou Janě __ roky a všem třem sourozencům bude dohromady __ let.
Úloha 1: Ivo má 3 krychle, Eva 2. Dohromady mají 5 krychlí. Více krychlí má Ivo.
Úloha 2: Postavím komín ze 4 krychlí.
Úloha 3: Goran má pětikorunu a dvoukorunu, Petr má dvě dvoukoruny a korunu.
Úloha 4: Janě budou 2 roky a všem třem sourozencům bude dohromady 9 let.
Různorodost úloh vede k různorodým řešením. Děti k řešení hojně využívají i matematická prostředí, ve kterých se běžně pohybují. Na síle nabývá argumentace a takový zápis, který je srozumitelný nejen řešiteli. Matematická náročnost se zvyšuje postupně. Viz úlohy 10–11.
Úloha 5: V únoru snížili cenu zimního zboží o polovinu, v dubnu snížili opět o polovinu. Kolik korun stály rukavice v květnu, když jejich cena v lednu byla 300 Kč?
Úloha 6: V dubnu snížili cenu rukavic o polovinu. Kolik korun stály rukavice před slevou v únoru, když jejich cena po slevě v květnu byla 80 Kč?
Úloha 7: V únoru snížili cenu zimního zboží o polovinu, v dubnu snížili opět o polovinu. Kolik korun stály v lednu rukavice, když jejich cena v květnu byla 60 Kč?
Uvedeme jednu situaci, jak úlohu řešila skupina dětí. Tonda k řešení použil graf:
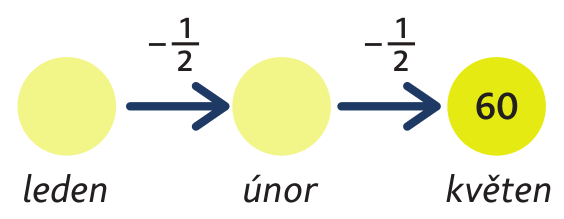
Z předchozích zkušeností s podobnými úlohami již věděl, že zde „jde od konce“. Číslo 60 chápal jako polovinu z ceny v únoru. Zjistil cenu rukavic v únoru, tedy 120 Kč. Částku 120 chápal jako polovinu původní ceny rukavic v lednu. Díky grafu uměl svou úvahu ukázat i ostatním přesto, že z matematického hlediska lze grafu ještě leccos vytknout. Míša rozuměla úvaze Tondy, ale protestovala. Graf jí nefungoval pozpátku. Ptala se: „Co znamená 60 plus polovina?“ Adam namítl, že to je jako 60 + 60, tedy 60 . 2. Míša upravila graf:

Nyní se radovali všichni. I ti, kteří měli původně názor jiný. Tato série úloh zaujala děti tak silně, že později samy vytvořily úlohu 11.
Úloha 5: Rukavice stály v květnu 75 Kč.
Úloha 6: V únoru stály rukavice 160 Kč.
Úloha 7: V lednu stály rukavice 240 Kč.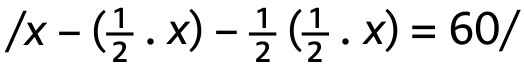
Do popředí se zde začne dostávat matematický jazyk. Na základě získaných zkušeností volí často již žáci u úlohy 7 k řešení jazyk matematický. Je dětem totiž srozumitelný. Vnímají ho jako silný matematický nástroj, který jim usnadňuje situaci.
Např. únor: 1/2 z x = 60, x = 120; leden: 1/2 z y = 120, y = 240.
S přibývajícími zkušenostmi bude časem řada dětí podobnou úlohu řešit pomocí jedné rovnice.
Úloha 8: Dnes jsou Bedřichovi 3 roky. Když mu bude tolik, co je dnes Adamovi, bude mít Adam 19 let. Kolik let je dnes Adamovi?
Úloha 9: Tatínek a maminka váží dohromady 171 kg. Tatínek váží o 60 kg více než maminka. Kolik váží maminka?
Úloha 10: Z kohoutku kape voda rychlostí 1 centilitr za 12 minuty.
a) za jak dlouho zbytečně odteče 1 litr?
b) kolik vody zbytečně odteče za 5 dnů?
Úloha 11: Zimní bunda byla zlevněna o 20 % a následně o dalších 20 %.
a) jaká byla konečná cena, když původní cena byla 3 200 Kč?
b) jaká byla původní cena, když nová cena byla 2 400 Kč?
Úloha 8: Adamovi je 11 let.
Úloha 9: Maminka váží 55, 5 kg.
Úloha 10: a) Litr vody odteče za 50 minut, b) Za 5 dnů odteče 144 litrů vody.
Úloha 11: a) Konečná cena bundy je 2048 Kč. b) Původní cena bundy byla 3 750 Kč.