Prostředí:

Prostředí:
Od sčítání až k soustavám rovnic
Počítat „sloupečky příkladů“ většinu žáků nebaví. Proto jim předkládáme úlohy na sčítání a odčítání vložené do různých prostředí.
Děti se učí tím lépe, čím více smyslů zapojí. V předškolním věku získávají zkušenosti s tím, že sloučením dvou množství vzniká něco nového. Klíčová je přitom možnost si všechno osahat, prohlédnout a sám vyzkoušet.
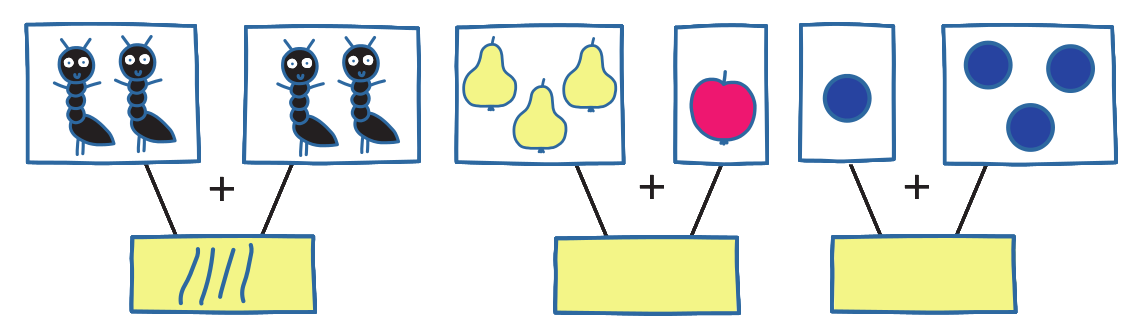
Úloha 1: Vezmeme zapnutou mikinu a zvedneme ji tak, aby se dolním okrajem dotýkala podložky. Jedno dítě vhodí do levého rukávu malý počet kamínků, druhé dítě vhodí několik kamínků do pravého rukávu. Kolik kamínků vypadne dole?
Náročnější obměna: Dítě vidí, kolik kamínků se vhodilo do jednoho rukávu, ale nevidí, kolik dáváme do druhého. Ukážeme mu až kamínky, které vypadly dole. Kolik kamínků jsme hodili do druhého rukávu?
Tato hra se dá hrát například s rozdvojkou plastového potrubí nebo s trychtýřem, kam se nevhodí všechno naráz, ale napřed první hromádka a pak druhá.
Na začátku 1. třídy děti neumí psát číslice, což jim ale nebrání učit se rozumět počtu a znázorňovat své výpočty na papír. Zatím pomocí čárek nebo teček připomínajících borůvky.
Důležité je hovořit s dítětem klidně a beze spěchu, abychom poznali, jestli rozumí, co znamená přidat, dát dohromady, ubrat apod. Zda přitom zapisuje čárky, puntíky, nebo číslice není podstatné. Cílem je směřovat k porozumění, že tři a jedna jsou čtyři, a je jedno, jestli jde o slony, slepice, nebo tečky.
Časem se objeví i náročnější úlohy. Spojením dvouřádkových trojúhelníků se pomaličku dopracujeme k víceřádkovým. Celý proces od jednoduššího ke složitějšímu v mysli dítěte zraje delší dobu. Opět se vyplácí nespěchat. Ukazuje se, že nejúčinnější pomocí je naslouchat dětem, jak úloze rozumí, a nechat je mluvit mezi sebou.
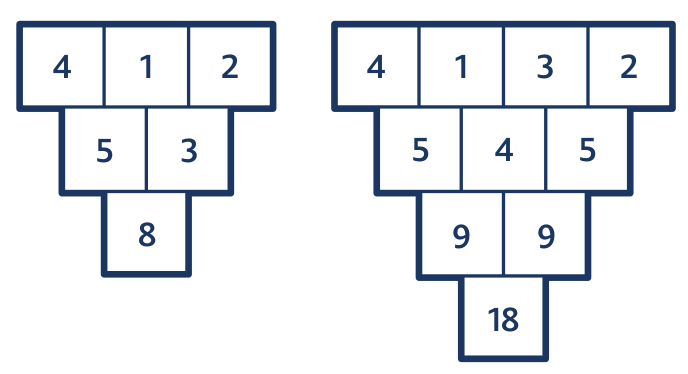
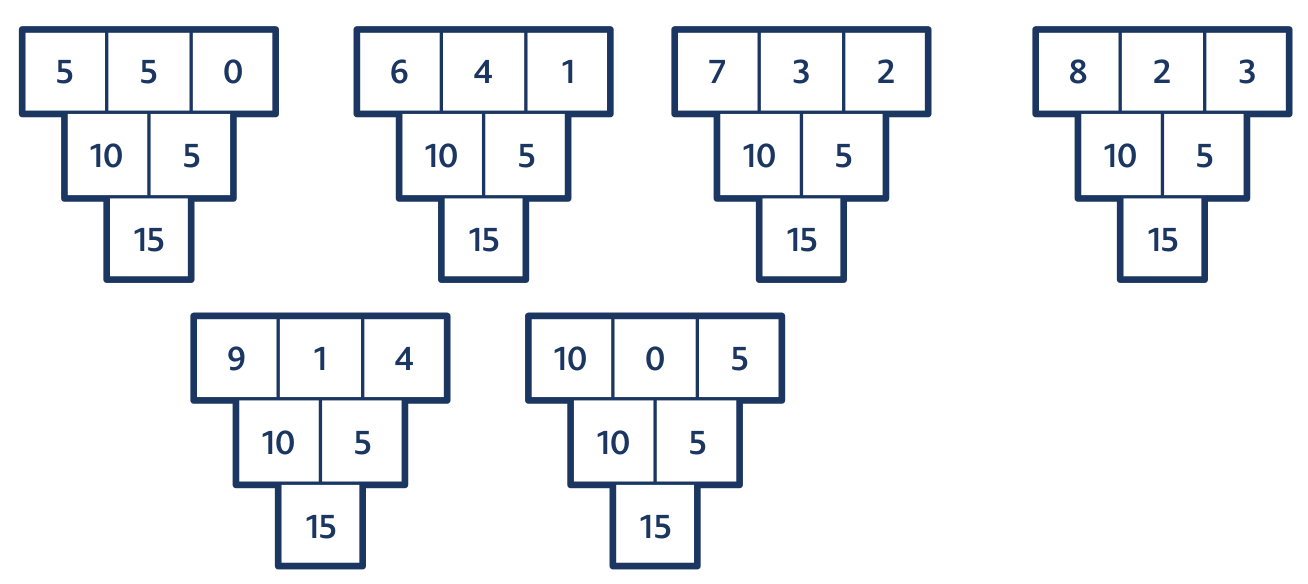
Úloha 2: Doplň.
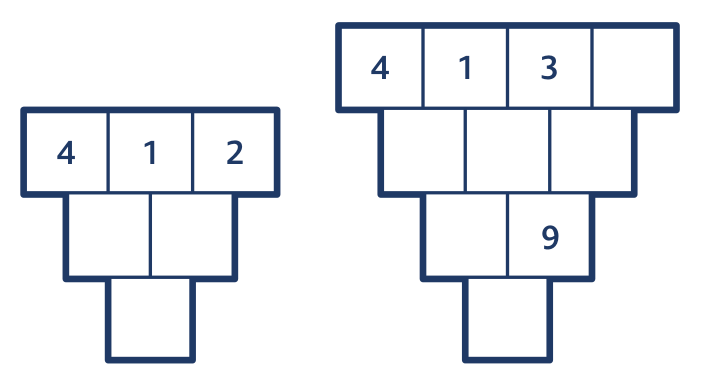
Při řešení prvního z trojúhelníků udělá žák tři výpočty: 4 + 1 = 5, 1 + 2 = 3 a 5 + 3 = 8. U druhého trojúhelníku musí čtyřikrát sčítat a dvakrát odčítat.
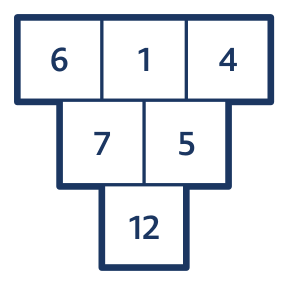
Úloha 3: Vrať neposedy zpět.
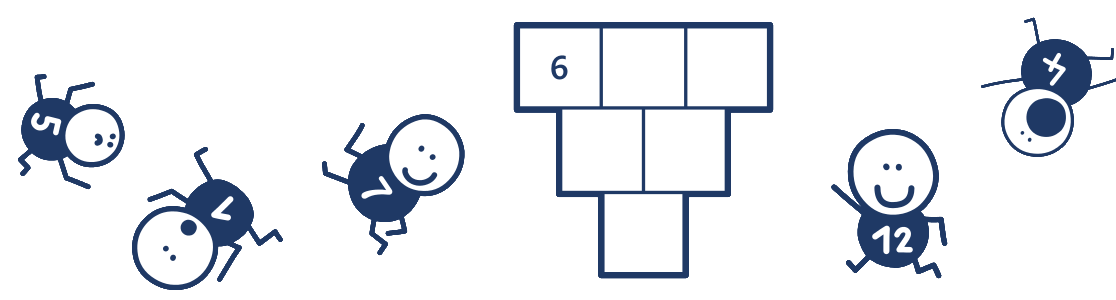
Žáci používají metodu pokus – omyl, která je základem objevování nejen v matematice. Například objeví, že největší číslo (zde je to 12) je v dolním poli.
Úloha 2:
Úloha 3:
Objevují se výzvy, které vedou žáky k novým zkušenostem a objevům. Například v následující úloze získávají zkušenosti z oblasti kombinatoriky.
Úloha 4: Najdi všechna řešení.
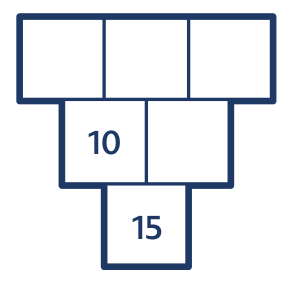
Po několika náhodných pokusech žák objeví, že v prostředním poli prvního řádku mohou být čísla 0, 1, 2, 3, 4 a 5 a žádná jiná. Pak jiný žák navrhne počítat i se zápornými čísly a najednou se ukáže, že v takovém případě má úloha „strašně moc“ řešení.
Žáci rychle získají zkušenost, že k výpočtu trojúhelníku se 6 čísly je nutno zadat 3 čísla. Jsou ale případy, kdy řešení nejde rychle najít.
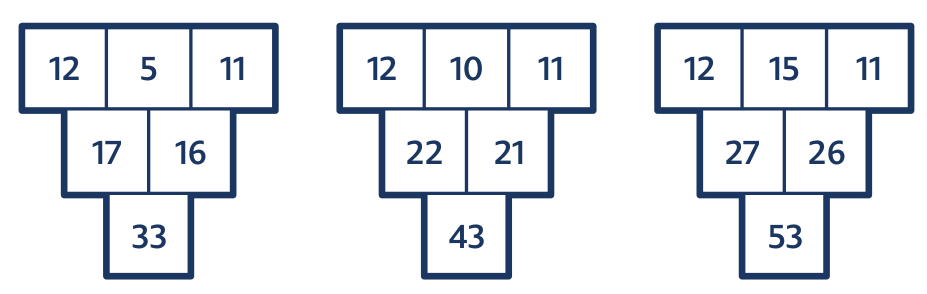
Úloha 5: Doplň.
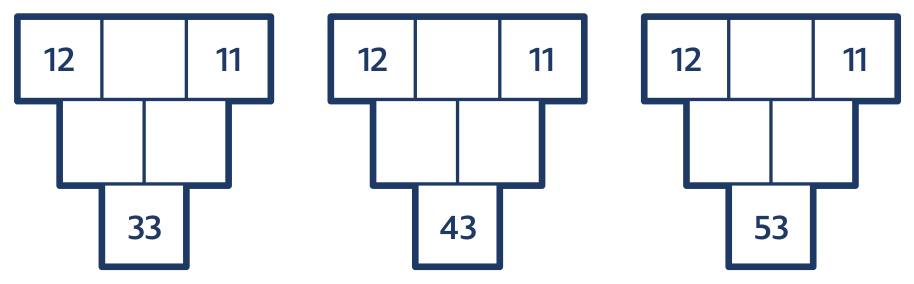
Metodou pokus – omyl žáci najdou dva řešitelské postupy: rozloží dolní číslo na dvě sousední čísla (tedy 33 = 17 + 16, 43 = 22 + 21 a 53 = 27 + 26), nebo najdou pravidlo, jak z daných čísel najít prostřední číslo v horním řádku.
Dalším krokem je přidání podmínky. Pak můžeme modelovat i soustavu lineárních rovnic.
Úloha 6: Doplň tak, aby součet dvou čísel ve vybarvených polích byl 9.
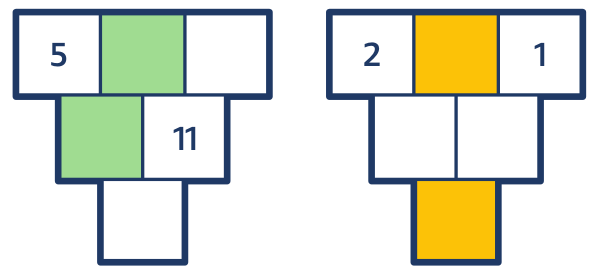
Rychlejší žáky vede učitel k objevování vztahů (například tím, že změní požadovaný součet 9 na jiný). Pomalejší žáci při používání metody pokus – omyl procvičí počítání a svým vlastním tempem vylepšují své řešitelské strategie.
První úloha modeluje soustavu rovnic x + y = 9, y – x = 5. Druhá soustavu rovnic x + y = 9, 2x + 3 = y.
Úloha 4: Pokud dosazujeme jen kladná celá čísla nebo nulu, je číslo v prostředním poli horního řádku jedno z čísel 5, 4, 3, 2, 1, 0.
Úloha 5:
Úloha 6:
Objevují se náročnější podmínky, které se týkají například součtu čísel v řádku nebo součtu všech čísel v trojúhelníku. Následující úlohy patří k těm náročnějším.
Úloha 7: Součet všech šesti čísel součtového trojúhelníku je 28. Součet tří čísel prvního řádku je 6. Najdi tento součtový trojúhelník. Najdi dvě řešení.
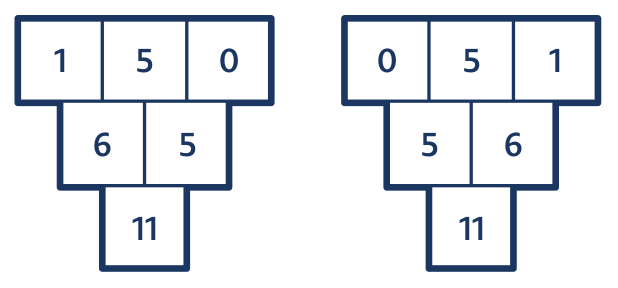
Úloha 8: Z vyřešeného trojúhelníku utekla čísla

a ještě jedno číslo, které uteklo z papíru úplně. Jak vypadal ten trojúhelník?
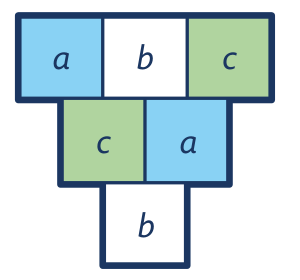
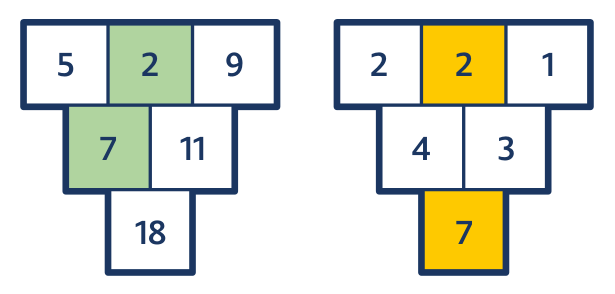
Úloha 9: Doplň tak, aby součet dvou čísel v zelených polích byl 10 a součet dvou čísel v modrých polích byl 11.

Žáci rychle odhalí, že úloha nemá řešení. Pak přijde hlavní výzva: Jak to dokážeš?
Úloha 7:
Úloha 8:
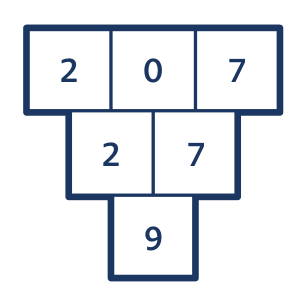
Úloha 9: Záludná úloha, která nemá řešení. Označme čísla horního řádku a, b, c. Pak součet čísel v modrých polích je a + (b + c) a součet čísel v zelených polích je (a + b) + c. Je jasné, že oba součty jsou stejné.