Hejny method is based on respecting 12 key principles, which it combines into a coherent approach enabling children to discover mathematicsby themselves and with enjoyment. It builds on 40 years of experimental work and puts into practice historical insights and notions about the teaching of mathematics, from Ancient Egypt through to the present day.
1. BUILDING SCHEMATA
CHILDREN KNOW MORE THAN WE HAVE TAUGHT THEM

Do you know how many windows there are in your house? Probably not by heart... but if you give it some thought, you will be able to come up with an answer. And your answer will be correct. That is because you have a schema - in other words, a plan - of the house in your mind. Children also have schemata in their minds. The Hejny method strengthens and interlinks these schemata, and infers general patterns from them. Children soon realize that half is also a number (0.5), and they do not find commonly “problematic” fractions problematic at all.
In real life, as well as in mathematics, mental schemata are main instrumental in decision-making. They permeate human thought and action; they determine what we set as our goals and how we evaluate. Many patterns that relate to the schemata of our everyday lives also relate to mathematical schemata.
What is a schema?
In very simple terms, a schema is a collection of interrelated pieces of knowledge that we have about a familiar environment. The following illustration will help to explain this further:
If someone asked you how many doors or carpets you have in your house, you probably couldn’t come up with an immediate answer. Yet after a moment’s thought you would be able to answer with confidence. You would have taken a mental walk through all the rooms and counted the relevant objects. These facts, along with many more pieces of information, are stored (just in case) in your mind, as a set of information that we call the schema of your house.
The schema of a house is constructed gradually, as a result of the activities that you do in the house. Different people perceive the same environment differently: the relevant schemata in their minds differ, even though the environment is identical. Activities take place in time but schemata change only little by little. House-related activities that we focus on (e.g. repairing something in the house) contribute to the development of the house schema more than activities that are centered around a different object (e.g. watching TV).
There are a whole range of schemata in our minds: the schemata of our house, the town we live in, the building we work in, the shopping center we shop in, the set of our relatives, the set of our friends, the collection of books in our bookcase , and so on. Each of these environments contains a large number of objects, relationships and sub-schemata. Each environment has unique characteristics, but many of the more general objects, concepts and relationships will be found in various environments and their schemata. For instance, the relationship “like” is not only present in the schema of interpersonal relationships, but also in the house schema because we like certain places or things in it.
Our method uses schemata such as a bus, walking, family, and so on: schemata that we have all formed on our own during our childhood. Using these schemata, children are able to discover the world independently and acquire autonomous knowledge, which is of lasting value for them.
MATHEMATICAL SCHEMA
A basic mathematical schema is the first more general understanding that originates from several concrete experiences; it is usually accompanied by the aha-effect.
Mathematical schemata are strongly interrelated. For example, the schema of the rational number concept emerges from linking the schemata of natural number, fraction, decimal number, and negative number concepts.
Moments of discovery and internal tension are decisive in the process of refining a schema. Think, for instance, of a 6 year old who has just found out that a half is a number, or of a 10 year old who discovers that a quadrilateral does not have to be convex, or that it is possible to form a triangle with an arbitrarily long perimeter and an infinitessimally small area. In practice, these formative moments of internal tension most often occur in class as a result of discussion about the difference between various pupils’ opinions.
GENERAL CHARACTERISTICS OF SCHEMATA
- Schemata are usually formed spontaneously, as a consequence of the person’s needs. If there is no need, the schema will not be formed.
- Schemata of one and the same thing will differ in different people’s minds. These differences can lead to misunderstandings.
- People who solve a problem together can, through interaction, find a better solution than they would have, had they solved the problem individually. Furthermore, a person who knows about other people’s schemata can make use of their knowledge.
- When something appears in a schema at an opportune moment and repeatedly, it will persist there for a long time. When something appears at an unsuitable moment or comes up only seldom, it will soon disappear from the schema.
- Parts of a schema that are only infrequently used need to be accessible in external memory so that they can be accessed when necessary. External memory frees up intellectual energy for more demanding tasks.
TEACHING BASED ON BUILDING SCHEMATA
Building schemata of mathematical concepts, phenomena, processes and situations in the mind of each pupil is what lies at the heart of a teaching method that strives to maximize autonomy in the pupil’s learning process. This method can be referred to as Schema-oriented Education, and is commonly known as Hejny method.
2. WORKING IN ENVIRONMENTS
LEARNING THROUGH REPEATED VISITS
When children know an environment and feel comfortable in it they do not get distracted by unfamiliar things. They focus fully on the task at hand, and are not bothered by unknown concepts. Each of the roughly 25 implemented environments (family, bus journey, stepping on playground, etc.) functions slightly differently. The environment based system takes into account the children’s different learning styles and the workings of a child’s mind. The child is then motivated to experiment further.
An environment contains a sequence of connected problems revolving around the same theme. A variety of mathematical phenomena are present in the problems. Each environment also offers problems that incorporate several mathematical phenomena at once. The problems encourage experimentation and discovery.
An environment contains a sequence of connected problems revolving around the same theme. A variety of mathematical phenomena are present in the problems. Each environment also offers problems that incorporate several mathematical phenomena at once. The problems encourage experimentation and discovery.
ENVIRONMENTS SUPPORT PUPILS IN ACQUIRING NON-FORMAL KNOWLEDGE
Pupils encounter each mathematical phenomenon frequently, in different contexts, in different environments, and at a different level of difficulty, which is adjustable to individual pupil’s needs. This enables each pupil to find their own way towards a good understanding of mathematics.
ENVIRONMENT THEMES ARE ENTICING
Working in environments also increases children’s motivation to work. Pupils find the themes of the environments attractive. Typically, they perceive the endeavor as play rather than serious work. They do not even notice how many individual exercises they have solved while experimenting. This does not commonly occur when completing exercises in traditional mathematics textbooks because these consist of problems of a similar type and are suitable for training memory.
Most problems in our textbooks encourage pupils’ creative activity. Children are actively engaged, and can experience a feeling of satisfaction with their own work. Diverse and multifaceted problems at an appropriate level of difficulty become fun challenges: they stimulate and cultivate the desire to figure something out, to discover something, to learn something.
EXPERIENCE-BASED
Some environments build directly on children’s experience of the real world – for instance, the Stepping, Staircase, Family, and Bus environments. Others employ activities that children enjoy doing – solving anagrams, brainteasers, crossword puzzles, playing games – for example, verbal arithmetic puzzle, Spiderwebs, Snakes, Addition Triangles, Multiplication Squares, Neighbors, Father Woodland’s Animals, Arrow Diagrams, ”I’m thinking of a number”, Coloured Triplets, and Imp Numbers.
Whether we perceive an environment as experience or as play, the most important thing is that it is intimately familiar and simple, like, for instance, building with blocks. More likely than not, all of us experienced this activity in our childhood. Building with blocks can be further expanded on through the Building Blocks environment, and this particular kind of activity-play can be used for calculating the volume or surface of cubes.
NO FEAR OF MATHEMATICS
Pupils get to know the themes of individual environments through simple problems. These problems gradually increase in complexity and each environment gets richer and richer. Children work in the environments repeatedly, gaining confidence, and letting go of their fear of mathematics, as they discuss and revise their ideas with their peers.
An unquestionable advantage of working in a familiar environment is formulating problems in a plain and concise manner. The role of the teacher shifts from a wisdom-holder to a problem-presenter and class-work manager. It is the pupils who are centre stage.
3. INTERLINKING TOPICS
NOT ISOLATING MATHEMATICAL PATTERNS
We do not present isolated information to pupils: it is always present in a familiar schema – a schema the children can recall at any time. We do not set mathematical phenomena and concepts apart, but we adopt different strategies for solving them. Children choose on their own what suits them best and what feels most natural. You will not hear any of the typical: “But, teacher, we did that two weeks ago, we do not remember it any more...“
When we connect the individual topics with each other, especially using our own experience, we are easily able to deduce or recall a particular piece of knowledge. Conversely, when we learn specific facts or rules separately without really understanding them, we might, eventually, not be able to recall them at all.
When information logically interlinks
If we wanted to learn the schema of our house by learning about the windows in September, about the kitchen in October, about the carpets in November, and about the lights in December, in January we would have to review everything that we have forgotten about the windows, the kitchen, and the carpets. However, as we learn about our house directly in action, through everyday activities that are complexly interconnected, we can recall our house and its parts whenever we please.
That is so because we take an active part in these activities. They are naturally linked to different parts of the house, and a number of sub-schemata are interrelated with those parts. For example, hanging pictures on the wall is connected with the living room sub-schema and the windows sub-schema. Before we hang a picture, we want to find out where the daylight, and later the lamp-light, would be coming from; we might also consider how well the picture would match the existing decor, and so on. We know our house well, and we know its individual parts, even though we have never learned about them and never specifically focused on them. All this information is stored in the house schema and we can retrieve it at practically any time, even if it may take us a moment.
DIFFERENT SCHEMATA FACILITATE BETTER UNDERSTANDING
Our mathematics works analogically. We learn about new concepts, processes, problem-solving strategies, and phenomena in different environments, and we gain a good understanding of them by putting the puzzle-pieces of partial knowledge from the various environments, and from the various activities, together.
We will show two examples here. In the first example, we will show how one activity links to various areas; in the second example, how many different activities facilitate the formation of one piece of knowledge.
1. PAPER-FOLDING
In a very simple activity, such as folding a square-shaped piece of paper into two triangles, children use their experience to form:
-
geometric concepts – a square; a triangle; an isosceles right-angled triangle; the diagonal of a square; a vertex and the side of a triangle; the hypotenuse of a right triangle; area (a square can be made up of two triangles);
-
geometric relationships – congruence of triangles; a square can be decomposed into two isosceles right triangles, and vice versa; the diagonal of a square is longer than its side;
-
arithmetic concepts – number 2, i.e. two triangles; a fraction as a part of whole, i.e. a half of a square.
While manipulating the piece of paper, and trying to fold it as precisely as possible, children also work on their motor skills, which will be beneficial later for construction problems. This is a crucial point in all the problems presented through different environments – by solving a problem, children not only practise their calculation skills, but they also learn something on top of the problem’s main focus area. Each environment endows mathematics with something unique.
2. ADDITION AND SUBTRACTION IN DIFFERENT ENVIRONMENTS
In this second example, let us look at addition and subtraction, and the varied opportunities a child is given to encounter these operations:
-
activities in the Stepping and Staircase environments (making steps, clapping, counting off in the rhythm of steps, recording steps by drawing arrows);
-
acting and solving problems in the Bus environment (passengers getting on and off the bus);
-
working with Father Woodland’s animals (balancing out the strength of two teams);
-
in Spider Webs and other environments that deal directly with numbers (structural environments);
-
in geometric environments, which do not deal directly with numbers, such as Tiles (choosing the number of tiles needed to cover a specific floor), Wooden Sticks (take three sticks and make a triangle, take two more and make two triangles), Building Blocks (construct a building with three cubes in the first floor and two cubes in the second floor) etc.
Each of these environments contributes in a unique way to the understanding of the concept of a number, and of the basic operations of addition and subtraction. As a bonus, each also creates the conditions for a different problem-solving strategies.
4. CHARACTER DEVELOPMENT
SUPPORTING THE CHILD’S INDEPENDENT THINKING

One of Professor Hejny’s main motives for creating a new teaching method was to protect pupils from being manipulated throughout their lives. For that reason, teachers using the method do not pass on ready-made knowledge in their lessons, but, rather, teach children how to reason, discuss, and evaluate. The children learn to know themselves what is right for them; they respect each other, know how to make decisions, and accept the consequences of their actions. Along with mathematics, they naturally discover principles of social behavior, and grow morally.
SCHOOL AS A SCHOOL OF LIFE
School is a setting in which children spend a substantial part of their life. It influences their mental and personal development. Aligning educational goals with this development is essential because many of its key moments take place in school.
We strive to build on our deep understanding of the child psyche and to respect the needs and patterns of the children’s growth. We try to bring education, social education, children’s school responsibilities, their formative interests, the teachers’ goals and the pupils’ needs into harmony. Teaching mathematics according to the Hejny method fully draws on the pupils’ personal potential, while encouraging, motivating and guiding their development.
FROM MATHEMATICAL DISCUSSION TO SOCIAL ATTITUDES
The newness of a school setting, and the demands and requirements that pupils are subjected to from the beginning of their schooling experience compel them to communicate with peers and to help one another. Consciously or not, they discover solidarity and the need to belong, and they assume common attitudes and procedures. Classrooms are places where the foundations of pupils’ social interaction and social life are formed.
The main bearer of school requirements and assigner of duties is the teacher: his or her role is crucial in the above described process of formation. In common practice, this role is prevalently dominant, in some cases even oppressive. The standard collective reaction of a group of pupils is to adopt an authority-dependent strategy, or possibly a strategy of rebellion against authority, and of resistance. When a teacher adopts this approach in the long-term, the pupils’ social attitude and behavior become distorted. That distortion will project into the children’s lives outside school, with negative social consequences.
Compared with traditional teaching, the Hejny method dramatically changes the positions and roles of both the teacher and the pupils in the class. The teacher’s dominance is suppressed as he or she becomes a manager of the children’s mental work, work that largely takes the form of communication. This benefits the development of the children’s mathematical knowledge while also cultivating their natural social skills in the desired manner.
WHICH SOCIAL SKILLS DOES THE HEJNY METHOD CULTIVATE?
-
Children are attentive and sensitive to their peers. When they explain ideas to one another they are expected to try to understand the ways others may think and why an error may have occurred. This leads to better mutual understanding.
-
Classmates’ ideas and opinions serve as inspiration or an extension of the child’s own thoughts.
-
We encourage children to discuss in a civilized and unemotional manner. We use disputes and mistakes to help the entire class progress as a community. Children often experience situations in which the majority is not right. We embrace diversity of opinions.
-
We try to lead children towards understanding figures of authority as the architects of the pleasant and creative environment in which the activities of the class and its members take place.
-
Children are guided towards self-knowledge and self-assessment (e.g. in graded-problem tests).
REACHING TRUE MATURITY THROUGH INDIVIDUAL DISCOVERIES
The Hejny method leaves the fundamental creative work of mathematics up to each child. Mathematical discoveries and achievements are either the results of the child’s own activity or are revealed in conversation with peers. The pupil alone can, to a large degree, choose the level of difficulty and the extension of the problems he or she solves, and later may also choose the difficulty of homework assignments or test. The teacher supports, but does not direct, the individual pupils’ work.
It is important that pupils themselves determine the pace, direction and extent of their work. This not only positively supports their mathematical cognitive development, but also improves and enlivens their opportunities to grow and improve. The Hejny method seeks to encourage the unceasing desire to learn, and to grow, which frequently gets stifled during puberty if the changes in the child’s internal motivation are ignored. Furthermore, the method can positively influence the child’s life-long strategy.
WHERE MEMORIZING TAKES US
When the learning content comes from a child’s experience, when it is matched against classmates’ opinions, and when the child is involved emotionally, the content is better perceived and compared to the child’s personal opinions and attitudes, i.e. their individual system of moral values.
In contrast, learning by mechanically connecting pieces of formal knowledge, images, and notation does not make the child think about their own system of moral values. All children believe betraying a friend is immoral, yet it is acceptable to copy test answers when the test is only the means to achieving a suitable mark in the world of formal knowledge. That world is already separated from reality. Real life, with its rules and morality, is cut off from the strange universe of school responsibilities and school knowledge.
SOCIAL EDUCATION GOALS ARE SUPERIOR TO COGNITIVE GOALS
School is a place where the work ethic and social habits of children, who later become adult citizens, evolve and develop manifestly. The fact that, in our society, the standards for knowledge are higher than the standards for morals is more serious an issue by far than that of mathematics education. Our method demonstrates, however, that good teaching can be remarkably effective in this area too.
5.TRUE MOTIVATION
WHEN “I DON’T KNOW” AND “I WANT TO KNOW”
In the Hejny method, all mathematical problems are designed so that children “automatically” enjoy solving them. The right kind of motivation is the internal kind, not forced by any outside factor. Children find the solutions to the problems thanks to their own efforts. We do not take away the joy of personal success from our children. Thanks to the class spirit we foster, every pupil receives applause, even those who discover a given phenomenon or solution later than others.
Motivation endows the learning process with energy and direction, and thus plays a key role in ensuring its quality. A child with an intrinsic need to learn learns in a more intense, deeper, and more complex way than a child who is forced to learn.
In fact we do not call the latter motivation, but only stimulation. It is clear from the Latin origin of these words that the difference between stimulation and motivation is quite significant: motivation is derived from the Latin moveō – to move, while stimulation derives from the Latin stimulō – to urge or to goad. We understand motivation as a need to learn, a need that arises from the internal struggle between “I don’t know” and “I want to know”, “I don’t know how” and “I would like to know how” , “I have not tried” and “I would like to try”.
MOTIVATION IS INNATE
Children are curious. They have a strong desire to learn about the things that surround them. They ask about anything they come across. They have a neverending need to acquire new experiences, even if they bring pain: think of the scraped knees of a child who is learning to ride a bicycle. Motivation to learn is an innate characteristic of every child.
CHILDREN’S MOTIVATION IS DIFFERENT FROM ADULTS’ MOTIVATION
Children’s motivation differs remarkably from adults’ motivation. Many misunderstandings arise from this difference. A child’s motivation is:
- urgent – whereas an adult will often perceive the urgency of a child’s need as stubbornness or even impertinence;
- volatile – a child gets interested in everything within his or her field of attention; an adult’s motivation tends to focus on one particular object;
- wide-ranging – a child explores his or her relationship with individual areas of human activity and acquires experiences that will help him or her to choose a future career appropriately.
A pupil’s desire to learn in school grows both as a result of the happy aha-moments that they have experienced in the past, and from the conflict between “I don’t know” and “I need to know”.
TRADITIONAL VS. HEJNY METHOD
Stimulation, rather than motivation, is prevailing in a traditional way of teaching mathematics. The impulse to learn comes from the desire to earn a good mark, or the fear of a low mark, the desire to be liked by the teacher, or the noble intention of making their parents happy. Children who are motivated by the need to discover mathematics are rather an exception then the rule.
The Hejny method offers children a discovery of mathematics that is based on their own experience. They start off in an intimately known world, but are constantly motivated to move further. Thanks to their internal motivation they are willing to “transfer” from the real world to the world of abstract concepts, they adopt certain mathematical tools and use these to discover so-called “higher” mathematics.
6. REAL-LIFE EXPERIENCE
WE DRAW ON THE CHILD’S PERSONAL EXPERIENCE

We draw on the personal experience a child has been forming from the moment they were born: at home, with their parents, while exploring the world in front of their house, or with their playmates in the sandbox. We build on natural, concrete experience that a child can use to form general conclusions. For example, children “sew a dress” for a cube, automatically learning how many faces, vertices and edges the cube has, how to calculate its surface area...
No doubt you can imagine the progress of a child who, at first, is only able to show three fingers to indicate three objects, but is later able to write the digit 3, and later still can substitute this digit with the letter “x”. When we are guided by our own intimately personal experience, we are willing to enter a world of complete abstraction.
MATHEMATICS AS EXPERIENCE
Mathematics teaching aimed at schema-building is based, above all, on children’s personal experience. When they solve problems, children collect a range of mathematical experiences. When, for instance, a child tries to count three M&M’s, they count one, two, three, pointing at each M&M. He or she will count three apples, three people sitting at a table, three steps, or three claps in a similar manner. The child will then confer with a friend to find out their way of counting, before suddenly coming to the generalization: “Oh, three is always this many,” and showing three fingers.
Fingers become a generic model. They are a substitute model for all previous experiences. The child now knows that three cars is that many (three fingers), even when they cannot see the cars. As a result of these experiences, the child begins to feel ready to write three as a digit; he or she accepts the abstract symbol “3” and starts using it. However, the concept of “three” in the child’s mind is founded on clear numeric images. The child understands the abstract concept. The new piece of knowledge finds its place in the child’s existing structure of knowledge and he or she continues to use it.
MATHEMATICS IN INTIMATELY KNOWN ENVIRONMENTS
All the mathematical concepts incorporated into the various environments in the textbooks are designed to follow the principles described above. For example, in the “Stepping” environment pupils accumulate experiences with natural numbers, with integers, with the minus sign followed by parentheses, with equations, and with absolute value.
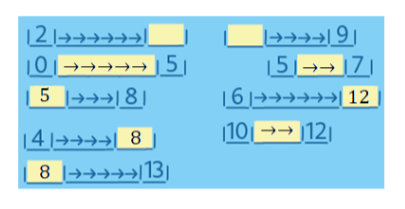
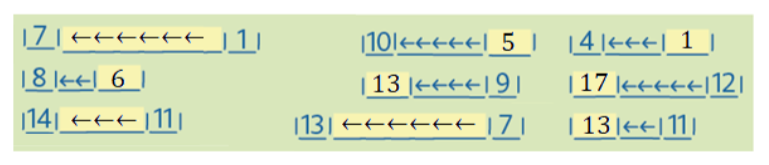
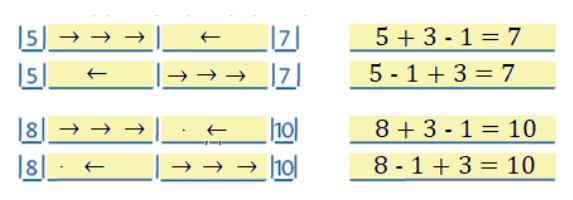
So when 10 year old children are presented with the problem: 2 − (__ − 1) = −1, a pupil may not know how to solve it using numbers. But they have by now gained an array of experiences with counting steps, and these will be used as a tool (the generic model) for the solution. The pupil translates the problem into arrow notation,
|→→|turn around| _____ |←|turn around| = | ←|,
then counts out the steps and finds the solution, as follows: two pupils are counting steps. The first pupil takes two steps forward, turns around, stays on the spot, then takes a step backwards, and turns around. The other pupil takes one step backwards and stops. What will the first pupil need to do to stand next to the other?
EXPERIENCE CAN ONLY BE GAINED, NOT TRANSMITTED
The trouble with acquiring experience is that experience cannot be transmitted. It can only be gained. There is only one way for a child to acquire experience in mathematics – by solving a problem. Any effort to make a pupil’s path to understanding shorter and to try to “pass on the experience” only addresses a momentary situation. No matter how noble our intentions, in reality we are doing the pupil a disservice. The knowledge we pass on to them is formal, and is only stored in their mind temporarily. In effect, it is not knowledge in the true sense of the word.
We can judge the accuracy of the above statements by referring to our own life experience. It should suffice to recall the frequency with which a mother scolds her child: “How many times have I told you..?” The child will still cut their finger, fall off a chair and not brush their teeth. They do not care how many times someone has told them. To learn to be careful, the child needs to gain experience; that is, they actually need to cut their finger or fall off a chair. You may recall the line “Do not lick the hand-rail,” from the movie Elementary School (Obecná škola). Just after watching this movie, we caught a boy who had got his tongue stuck to a fence pole because he did not believe that what he had seen in the movie was true.
EXPERIENCE THROUGH FAILURE
On the other hand, the advantage of learning through acquiring experience is that a pupil gains experience even when they do not manage to solve a problem. They benefit from the very fact that they have tried to solve the problem, and were mentally engaged in it.
No lesson is lost as long as the pupil is engaged in work. The pupil still acquires experience, even if they do not achieve a particular goal. They confirm that this particular way does not lead to a solution. They find out what other things they will need in order to solve the problem successfully. They realize, for instance, that they would benefit from knowing how to multiply small numbers. These situations are important for pupils; they will be able to capitalize on them in the future.
7. ENJOYING MATHEMATICS
ENJOYMENT SIGNIFICANTLY CONTRIBUTES TO FURTHER LEARNING

Experience speaks clearly: the most effective motivation derives from a child’s feeling of success, from their genuine joy of having solved an appropriately demanding task. It lies in the pleasure they gain from their sense of progress, or in the praise and respect they receive from others. Children who have this motivation do not experience the “mathematics paralysis” that has become legendary in traditional education. On the contrary, when they see a formula, they do not react with displeasure but with enthusiasm: I know this, I can solve this!
THE POWER OF INTERNAL MOTIVATION
We know from everyday experience that children with prevalent internal motivation are more independent thinkers and decision-makers than those with predominantly external motivation. The joy of thinking originates in personal discoveries. The mathematical environments in our textbooks are designed to facilitate discovery. Different environments ensure the success of different types of children.
The complexity level of the mathematical problems presented is set so that even less able pupils can experience the joy of success. These pupils are assigned problems whose difficulty level is appropriate for their skills. The word appropriate is extremely important here: the problem has to be easy enough for the pupil to solve it, but challenging enough that the pupil has to make an effort, and will experience joy when they have tackled it. This feeling then becomes the engine for further work and triggers the motivation to solve new problems and to work intellectually.
PLANTS DO NOT GROW WHEN PULLED EITHER
When knowledge is presented to, or even forced upon, a pupil -- who is expected to reproduce and imitate the knowledge they receive, and is denied the process of gaining their own experience -- such a pupil will be unwilling, or even unable, to acquire further knowledge using their own resources.
Such pupils will collect theorems and formulae and will become “intellectual parasites” (as expressed by Russian psychologist A. M. Matyushchin). Their autonomy and need to learn, which are the essence of motivation, are actually suppressed. It is impossible to speed up a child’s learning process by giving them ready-made knowledge, just as plants do not grow faster if we pull at them every morning.
8. PERSONAL KNOWLEDGE
IT OUTWEIGHS RECEIVED KNOWLEDGE

When a 6 year old is asked to build a square using rods, they pick up a first, a second, a third rod... these are still not enough, so they take a fourth rod and build a square. Then they decide to build a bigger square. They pick up more rods, and build the bigger square, beginning to understand that whenever they want to make a bigger square they will need four extra rods. They are now on their way to discovering the formula for calculating the perimeter of a square.
Our textbooks follow a conception different from those in standard textbooks. They are written with the belief that knowledge gained through personal reasoning has a higher quality than received knowledge. In our textbooks pupils discover mathematics themselves. The pathway of discovery takes the pupil from a personal experience to a concept. The pupil collects a range of experiences, which they talk about. He or she discusses the experiences with a classmate. They each explain their own theories, and subsequently test them on further problems. Throughout the process, they understand what they are doing.
BIG AND SMALL “PYTHAGORASES“
Fine, you might think, the discovery path is obvious in this case, but what about “higher” mathematics?
By the age of 10, pupils have cut pizza into slices, they have cut paper, and fit various pieces into a pie, a circle, or a chocolate bar, and have solved a variety of problems involving similar topics. They have never been told how to calculate part of a whole. Still, they know for certain how many minutes there are in a quarter, a third, a fifth, and two fifths of an hour. They know how to calculate both part of a whole and a whole from parts, in a range of situations.
A pupil is presented with a problem to find out how much 1/2 + 2/5 is. They may use, for example, a clock-face as an aid. They know that half an hour is 30 minutes. They know how to calculate that one fifth of an hour is 12 minutes, and so two fifths of an hour is 24 minutes. 24 minutes + 30 minutes is 54 minutes. They write 1/2 + 2/5 = 54/60. The numbers in this solution seem a bit high, so they reduce them, for instance by halving them. Now they have 27/30. The numbers can be further reduced to 9/10.
The pupil solves further problems in a similar fashion, records the solutions and discovers a trick. By creating a general mathematical pattern they discover “Pythagoras’ theorem” on their own. One pupil will find their “theorem” when they are ten, one between the ages of 11 to 14 in the fifth grade, another throughout grades six to nine; yet another pupil will not discover it at all: he or she will let a classmate explain it to them. They will think about it and accept it as their own. All three pupils, though, will discover the path not only to adding and reducing fractions, but also to mathematical patterns. Most importantly, they see their activity as meaningful. These pupils, too, will eventually convert the given fraction to ones with a common denominator. At the same time, they understand why they do so and why it works as it does. Their knowledge is permanent.
YOU CAN DISCOVER INTEGRALS
So how, you may ask, will high-school students discover integrals? People who ask this usually have the integrals they themselves learned in school in mind. These commonly correspond with the Weierstrass approach to integral calculus. That particular theory is built on rigorous logical principles, using so-called “epsilon delta” definitions.
Our intention is to make use of more illustrative and more intuitive approaches, such as the Cavalieri principle. This principle is first discovered when calculating the area of triangles and the volume of solids. Later it can be used to experiment with areas of curvilinear objects defined by a parabola, a horizontal line and a vertical line (to be exact, lines that are parallel with the axes in the coordinate system), i.e. of certain “triangles with one bent side”. Students find out, for instance, how many times larger the blue object is than the red one. Next, they find out how many times larger the green object is than the blue one. By doing these calculations they discover the ratio for the areas of the red and green objects.
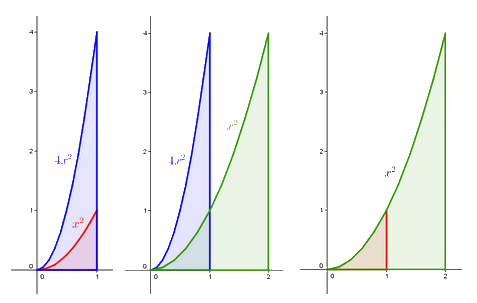
With the aid of further suitably chosen experiments, the students discover the trick for calculating the areas. Using the same trick, it is possible to find a method for calculating the area under many other curves and, finally, under any polynomial curve. In essence, this is what Cavalieri did two centuries before Weierstrass. By discovering these methods, students gain an understanding of the ideas underlying integral calculus.
FROM INDIVIDUAL REASONING TO ACCEPTING CONVENTION
Thanks to personal experience and logical reasoning, children are also ready and able to accept the conventional language of mathematics. “Ah!,“ declares a 7 year old after discussing a series of experiences multiplying small numbers, “if I want to find out how many wheels there are on four tricycles, I don’t have to write 3 + 3 + 3 + 3. I can just use the times sign!” This pupil understands the multiplication operation and accepts its mathematical language. They are proud of themselves, and they look forward to new problems. The linguistic path to mathematical discovery can be summarized as:
EXPERIENCE ⇒ MOTHER TONGUE ⇒ MATHEMATICAL LANGUAGE.
9. THE TEACHER’S ROLE
GUIDING AND MEDIATING DISCUSSION

The typecast image of a teacher is that of someone who possesses knowledge and skills, and lectures about them. The mathematics teacher knows mathematics, and can therefore explain mathematics to their students. Often, it really does work like this: the children listen to their teacher’s explanations, write down a few notes, listen to instructions about how to solve a new problem, and learn to use the new procedure. However, in our understanding of the teaching process, the teacher plays a dramatically different role.
The teacher’s role in lessons according to the Hejny teaching method is demanding, but in an entirely different way to that we are used to from traditional teaching.
ADVISOR RATHER THAN AUTHORITY
The teacher is not a lecturing figure of authority with knowledge and skills. Yes, the teacher does know and can do, but does not demonstrate this in any way. If anyone explains things, it is the pupil. The teacher is in charge of organizing the lessons, encouraging pupils’ work, setting appropriate tasks, sharing the pupils’ joy over their discoveries, and mediating their discussions. He or she also plans and supervises lessons such that each pupil has appropriate work to do. The teacher assigns challenging problems to especially able pupils, and helps less able students to find a problem-solving strategy. He or she is a tacit guide throughout the lesson, but does not assume the lead.
SWITCHING ROLES
If teachers want to adopt the Hejny method successfully, the adaptation of their own role is among the most difficult changes they must make. It is difficult to get used to the idea that it is the pupils themselves who discuss a problem after it has been presented in class. The pupils will often propose solutions that are unusual, incomplete or even wrong, but it is precisely those moments that are key to the pupils’ future understanding.
Working with error plays a key part here. The teacher does not evaluate individual proposals. He or she turns to the class and asks whether the other pupils agree or not, and why. Pupils thereby learn to analyze both their own and their classmates’ errors. A faulty solution leads them to discover a correct one. They gradually come to draw generalizations from their various mathematical experiences, deepening their knowledge and understanding of mathematics.
The teacher must not use their own knowledge to show pupils a shortcut in their learning process. When that happens, it results in gaps in the pupils’ understanding. These gaps are likely never to be filled, and will fail the pupil in the future. Any shortcut, even one with the best intentions, results in formalism, an illness whose symptom is the pupils’ apparent but temporary knowledge: the pupils only know what the teacher told them, and for as long as they can remember it.
TEACHER DOES NOT EXPLAIN
The teacher does not focus on preparing instructions when lesson planning. Instead, they contemplate which problems will most help their pupils to understand. They work with their pupils’ varied levels of ability, knowing that they have some more able, and some less able students in their class. They develop the technique of preparing so-called graded problems, i.e. problems with different levels of complexity, to suit all types of pupils in the class. They learn to complement a textbook problem with both easier and more challenging variations.
10. WORKING WITH ERROR
AVOIDING UNNECESSARY ANXIETY

If a child was forbidden to fall, they would never learn to walk. Making and analyzing our own mistakes forms a deep experience, which helps us to better remember the knowledge we have acquired. We use errors as a means of learning. We encourage pupils to identify their own mistakes, and we teach them to explain why they made them. The trust fostered between teachers and pupils strengthens the children’s delight in accomplishing their tasks.
Error is a natural phenomenon that accompanies any human activity, especially when we try the activity for the first time. When error is handled well, it is a welcome companion on the road to understanding. When we recognize it, and identify its causes, our ability to conduct the given activity better in the future increases.
Throughout the Hejny learning process we do not condemn error, we defend and welcome it. We appreciate error as an aid to each pupil’s true understanding. We are aware that one learns from one’s mistakes, and want to implement this process fully in our teaching and learning (not only in mathematics).
WHEN THE TEACHER FEARS ERRORS
In traditional teaching, error is usually understood as an unwanted phenomenon. Teachers themselves are afraid of making a mistake. They feel responsible for their pupils’ potential errors (whether committed on the board or in an exercise book) so they are quick to point them out and correct them.
The pupils’ parents, who also perceive error as unwanted, increase the teacher’s fear of potential mistakes. In consultations, teachers more often talk about the mistakes themselves, rather than about their causes, or ways of preventing them from happening.
ERRORS ACTIVATE THE THINKING PROCESS
A teacher who teaches by instruction expects their pupils to repeat processes or rules that have been demonstrated or stated in class. Anything that deviates from these processes is usually seen by the teacher as mistakes. This is detrimental to the development of the pupils’ independent thinking.
By treating error as an unwelcome phenomenon, teachers create an atmosphere in the class that blocks the children. Faced with the fear of committing an error, pupils prefer not to do anything. The teacher also does nothing to prevent error, other than exert pressure on the pupils. Some teachers even believe that punishment for errors encourages their pupils’ effort to learn and therefore improves their academic results.
However, reality does not confirm this assumption. It is true that pupils, out of fear, invest more energy in the subject matter, but most of this energy goes to waste because the pupils’ activity is then driven by, and focused on the need to protect themselves from punishment: pretending to be ill, cheating, lies, truancy or making excuses.
WE DO NOT FOCUS ON OUR MISTAKES, BUT WE LOOK FOR THE REASONS BEHIND THEM
When a pupil makes a mistake, say, in calculation, the teacher does not usually immediately see where it stemmed from. If he or she simply corrects the mistake, this does not help the pupil much. The fundamental question, i.e. why they committed this error, remains a mystery for the pupil.
If a teacher does not try to understand the source of an error, the correction is understood only in terms of teacher-authority. The pupil does not see where the fault in his reasoning is and will, naturally, commit the same error next time.
Mistakes should not discourage pupils. An error can and should be a useful experience. The teacher’s role is to help pupils learn from errors. Teachers who reprimand pupils for making mistakes make the process of learning new things more difficult.
WORKING WITH ERROR SIMPLY
If a pupil is afraid of making a mistake, the Hejny method teacher encourages the pupil by giving his or her own example: showing them where the teacher went wrong, and how they discovered the source of their mistake. Whenever a pupil points out a mistake made by the teacher, the teacher thanks the pupil for correcting the error, and rewards them with praise. Analyzing the (teacher’s) error out loud in front the class is highly effective. The pupils can observe possible ways of dealing with error, and will find such examples inspiring.
Intellectually, understanding the reasons behind an error is an effective way to grasp the nature of a phenomenon under investigation. This is not only true for pupils in school but also for famous mathematicians. They, too, committed errors and the discovery of the errors served as an important lesson for them.
USING ERROR TO FILL THE GAPS IN PUPILS’ EXPERIENCE
When teachers know how to work with pupils’ errors, they can exploit each mistake didactically. The teacher’s knowledge is both diagnostic and educational. Using their diagnostic skills, the teacher gauges their pupil’s error awareness (of whether and where the error occurred). Their educational skills comes into practice in order to repair the problem. When we find out that a pupil does not understand something, we enable them to fill in the gaps in their experience themselves.
11. APPROPRIATE CHALLENGE
TASKS FOR EACH CHILD AT THEIR LEVEL

Our textbooks present problems with varying levels of difficulty. Always allowing weaker pupils to solve some problems successfully precludes any feelings of anxiety and fear of future mathematics lessons. At the same time, we constantly provide the best pupils with further challenges, to prevent them from experiencing boredom. The teacher does not overburden these pupils with tasks. Instead, he or she assigns tasks that will keep the children motivated. The teacher chooses the tasks according to each child’s needs.
DIFFERENTIATION BASED ON DIFFICULTY
The problems in our textbooks are differentiated according to how difficult they are: for a problem that has got parts a) to f) we would like part a) to be solved by every pupil in the class without any help from classmates, part b) to be solved by about 90% of pupils, part c) by about 75 %, part d) 50 %, part e) 25 % and part f) perhaps only 10 %, or just one child in the class. The underlying idea is that each pupil is presented with an appropriate challenge. Weaker pupils will always solve some problems successfully, which will keep them from experiencing anxiety and fear. At the same time, even the best pupils are constantly challenged, not bored. Avoiding fear and boredom in mathematics lessons is our primary concern.
FOR THE WEAKER AS MUCH AS FOR THE STRONGER
It might seem that the stronger pupils make many discoveries, while the weaker ones are simply out of luck. The teacher plays a crucial role here. A good teacher recognizes that what for some pupils may be obvious, the weaker ones need to discover for themselves. The teacher will praise such discoveries and, by giving praise, he or she implicitly shows what mathematics is about. We want our teachers to praise pupils for thinking and ideas, and to share the joy of discovery with their pupils – discoveries appropriate to those individual pupils’ abilities.
Gifted pupils are of great concern to us. To let them accept boredom is a waste, not only of their individual potential, but also the potential of our entire community. We believe that gifted students need to find challenges in our textbooks and to be constantly engaged in an intellectual activity. Our teacher’s book contains problems that will give these pupils opportunities for ongoing development.
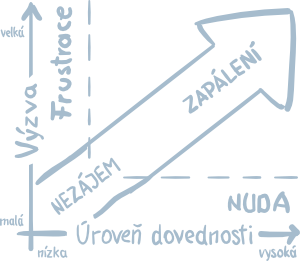
RESPECTING THE CHILD’S DEVELOPMENTAL STAGES
Our endeavor is informed by the field of psychology in order to create appropriate “steps up” in terms of the difficulty of different levels of problems. What is difficult for children is often perceived as simple to adults. As an example, think about solving a word-problem using an equation with an unknown. The decision to work with an unknown number requires a great amount of courage, and a child is not able to make this decision without first acquiring a lot of experience. Children are sometimes pressed into prematurely accepting the adults’ way of doing or understanding things. On the other hand, children at primary level are known to be able to contemplate things that adults have never considered, and which the adults might think too complex for the child’s age.
SELF-ASSESSMENT
We recommend that teachers create so called graded assessments. Such tests should contain similar problems at various levels of difficulty (e.g. three problems from one mathematics environment, marked as “easier”, “medium”, and “difficult”). Children will decide on the appropriate level at their own discretion. This means that they will assess themselves, i.e. they will practise self-assessment. Our goal is to enable each child to fully develop their character in all its complexity.
12. SUPPORTING COLLABORATION
ACQUIRING KNOWLEDGE THROUGH DISCUSSION

With the Hejny method, children do not need to wait for the solution to appear on the board. They work in groups, in pairs, or individually. Each pupil is able to share how he or she found their solution, and is also able to explain their working to the others. The solution emerges through collaboration. The teacher does not represent the authority who decides when the answer is right – and when the pupils can turn over another page in the book. Pupils build their own meaningful piece of knowledge, in a continual train of thought.
Most knowledge emerges in children’s minds as a result of their experiences and mutual discussion. Therefore, children need to be provided with space for collaboration and discussions in their lessons. This type of communication proves highly effective.
A choice of working styles
Each child is unique and so will prefer a different working style. Some like to work individually, others are more successful completing tasks in pairs or groups. There is no harm in giving the children this choice when a new mathematics problem is presented. Those who want to work independently will tackle the problem straight away. Those who feel more comfortable working with someone will find a partner. Needless to say, even the former will enjoy sharing the results of their endeavors with a classmate afterwards.
THE IMPORTANCE OF DISCUSSION
Discussion among pupils is indispensable, regardless of their stage in the learning process: whether they are just beginning to acquire a piece of knowledge, or are already confirming their own conclusions. Discussion brings out a variety of ideas, prompts, or even misconceptions that motivate a pupil to look for the correct solution. There is no authoritative figure who decides what the truth is. The adult simply observes and allows the child to form their solution and justify it to the others. Thus, each child constantly assesses different options and keeps thinking about the problem throughout the discussion. They build up a meaningful piece of knowledge that fits into their existing cognitive structure.
THE TEACHER’S ROLE
The teacher gives precedence to activities that encourage collaboration between the students. Each lesson is planned so that it provides pupils with space for collaboration. A variety of task types is important not only in terms of pupil typology but also in terms of the acquisition of new knowledge.
The goal, however, is not to vary these types of task as much as possible within one lesson. It is far more important to keep the lessons effective, while not allowing any particular task type to be left out in the long run.
The teacher’s main intention is to select task types that encourage the pupils to interact. Whether this interaction takes the form of discussion in pairs, groups, or the whole class is not an issue. The diversity of tasks and working styles ensures that the lesson is enjoyable and fun. No activity is endlessly repeated.
NO BARRIERS BETWEEN PUPILS
How different this approach is from the traditional class, in which a teacher strives painstakingly to stop pupils from copying. In that class, pupils are likely to be punished for trying to consult with their classmates, which often results in the pupils building barriers, or barricades, to prevent their classmates from copying. This fairly common scenario is entirely incompatible with the Hejny method, for which is vitally important to take any such barriers down, so that the children’s communication can flow naturally, in a civilized, objective, and seamless manner.

Komentáře