
Prostředí:

Prostředí:
Učíme se systematické práci
Děti mají rády stavebnice, s oblibou skládají různé vzory a mozaiky. Staví různobarevné věže z kostek nebo třeba kombinují oblečení pro panenku. Chlapci a děvčata tak přirozeně zjišťují, že ze stejného počtu stavebních dílů mohou postavit nepřeberné množství staveb, že ze stejné sady oblečků a doplňků pro panenky ji mohou připravit na různé příležitosti třeba jen změnou bot a ozdob.
Nejde nám o to, aby děti počítaly, kolik různých možností mají, ale aby si užily hru, rozvíjely svou kreativitu a hledaly různé možnosti. Stavíme si s dětmi, pobízíme je k záměnám různých dílků ve stavebnicích, ke kombinování oblečení panenek.
Vystřihněte tři trička (např. bílé, žluté a červené) a dvoje kalhoty (hnědé a modré). Dítě vyzvěte, aby zjistilo, jak může kombinovat jednotlivé kousky oblečení. V pondělí si vezme do školky modré kalhoty a bílé tričko. Co si obleče další den, aby bylo jinak ustrojené. Kolik dnů může být pokaždé jinak oblečené?

Zahrajeme si hru na bytového architekta, který má k dispozici parkety určitého typu a má s nimi pokrýt danou podlahu. Dítě zkouší, jaké možnosti položení má, jaké různé vzory může z parket vytvořit. Pro tvorbu dalších úkolů můžeme měnit barvy parket, jejich tvar, můžeme zvyšovat počet barev nebo počet použitých tvarů. Úkoly ztížíme nějakou podmínkou, např. že stejné barvy parket se mohou dotýkat jen růžkem.

Hra na obkladače: vystřihněte několik čtverců dvou barev – dlaždiček (místo nich můžete použít i dva druhy pexesa) a nechte dítě skládat různé vzory. Ty může zakreslovat na čtverečkovaný papír a porovnávat, zda se některý neopakuje.
Hledání různých možností přenášíme do reálného života. Děti s námi chodí nakupovat a rády za nákup platí. To využijeme k výzvě.
Úloha 1: Čokoláda stojí 24 Kč. V peněžence máš pouze pětikoruny a dvoukoruny. Kolika způsoby můžeš čokoládu zaplatit? Svá řešení zapiš do tabulky (počet mincí můžeš zaznamenat pomocí čísel nebo čárek):
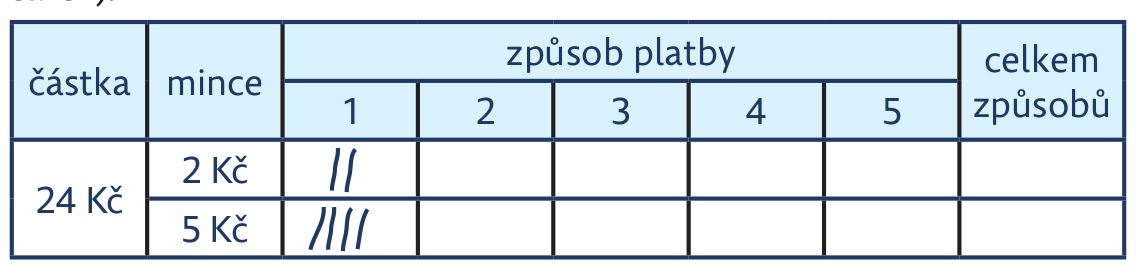
Úloha 2: Kolika způsoby můžeš zaplatit stejnou čokoládu, když máš v peněžence navíc ještě desetikorunu? Vytvoř si a doplň podobnou tabulku, jako je v úloze 1.
Úloha 3: Hledej různé možnosti, jak zaplatit dvě stejné čokolády, když máš v peněžence všechny druhy českých mincí.

Úloha 1:
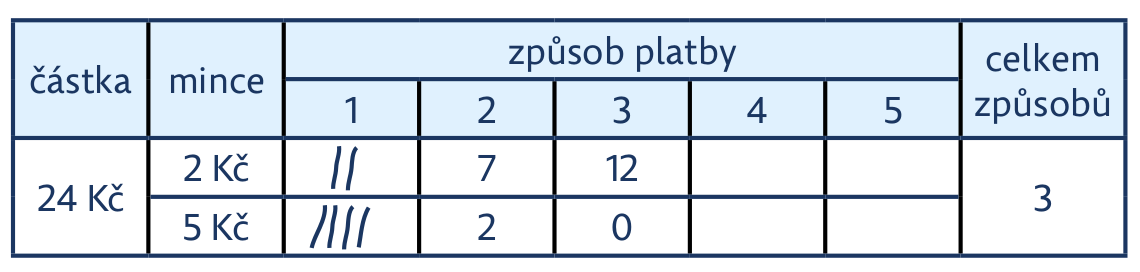
Úloha 2:

Úloha 3: Hledání mnoha řešení vede žáky k systematické práci. Pro zjednodušení můžeme k platbě použít třeba jen koruny, pětikoruny a dvacetikoruny. Pokud budeme opravdu uvažovat všechny české mince, existuje dokonce 394 možností, jak zaplatit 48 Kč.
S dětmi si zahrajeme hru „panna nebo orel“ a necháme je tipovat, co padne častěji. Výsledky si můžeme poznamenávat a zkoumat, zda některá strana mince padne častěji. Podobně můžeme házet hrací kostkou.
Házení mincemi nebo kostkou je velice důležité jako příprava na témata pravděpodobnost a statistika. Až na tato témata přijde řada ve škole, bývá už „dítě“ příliš velké na manipulativní činnost a často nemá čas ani chuť provádět skutečný pokus s mincí nebo kostkou. Bez těchto zkušeností si žák pravděpodobnost nezažije.
Úloha 4: Házej hrací kostkou. Hoď desetkrát a zaznamenej hozená čísla. Kolikrát padlo sudé a kolikrát liché číslo? Pokračuj v házení a udělej 50, 100, 200 pokusů. Bude častěji padat sudé, nebo liché číslo? Je to jen náhoda?
Úloha 5: Ze záznamů k předchozí úloze urči, zda padlo častěji číslo, které je násobkem tří, nebo jiné číslo.
Úloha 6: Hoď dvěma kostkami a sečti počet ok. V tabulce vyplň políčko nad příslušným číslem. Když hodíš 1 a 4, součet je 5, tak vybarvíš políčko nad pětkou. Odhadni, jak bude tabulka vybarvená po 100 hodech a správnost svého odhadu ověř s několika kamarády.
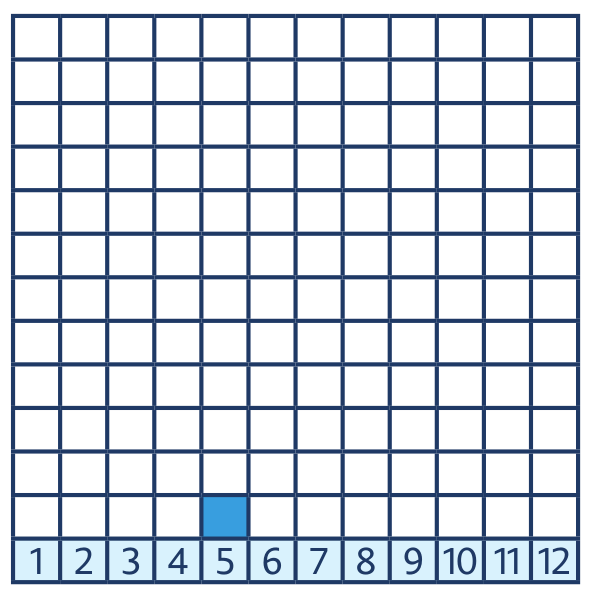
Úloha 7:
a) U kterých čísel v tabulce je sloupec nejvyšší?
b) U kterých čísel v tabulce je sloupec nejnižší?
c) Jsou předchozí výsledky zcela náhodné?
Úloha 4: Sudá i lichá čísla budou padat přibližně stejně často. Náhoda to není, protože na hrací kostce je stejný počet sudých i lichých čísel.
Úloha 5: Při větším počtu házení častěji padne jiné číslo, a to přibližně dvakrát častěji, protože na hrací kostce je násobků tří dvakrát méně než čísel jiných.
Úloha 6: Vybarvené sloupce vytvoří „pyramidu“ ohraničenou Gaussovou křivkou.
Úloha 7:
a) U čísla 7, případně u jeho sousedů.
b) U čísel 1 a 13, protože ta padnout nemohou.
c) Nejsou, protože způsobů, jak ze dvou čísel na kostce složit sedmičku, je nejvíce (6), pak následují čísla 6 a 8; 5 a 9; 4 a 10; 3 a 11; 2 a 12, která jdou složit pouze jedním způsobem.
Úloha 8: Když jsem přijela na návštěvu ke kamarádce Denise, nemohly jsme se rozhodnout, kam se půjdeme projít. Plánek čtvrti, ve které Denisa bydlí, je na obrázku. Dohodly jsme se, že na každé křižovatce hodíme mincí. Když padne panna (p), odbočíme na křižovatce vpravo, a pokud padne orel (o), vydáme se vlevo.
První den nám padla p, o, o, p, o a došly jsme do parku.
a) Kam dojdeme, pokud nám padne: o, p, p, p, o?
b) Co musíme hodit, abychom došly k řece?
c) Takto jsme chodily dva týdny, každý den jednou.
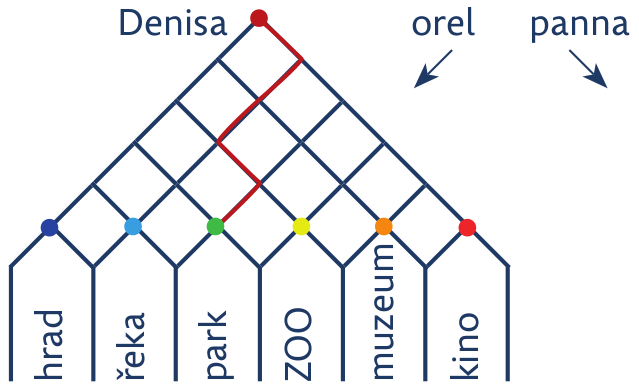
Udělej také 14 procházek a do tabulky zaznamenávej, kam dojdeš.

d) Je nějaké místo, kam zavítáme častěji? Pokud ano, tak proč?
Úloha 8:
a) Dojdeme do ZOO.
b) Musíme hodit 1 pannu a 4 orly (nezáleží, v jakém pořadí).
d) Nejčastěji navštívíme park a zoo, protože tam vede nejvíce různých cest. Naopak na hrad nebo do kina vede cesta jediná.