
Prostředí:

Prostředí:
Rozvíjíme prostorovou představivost
Toto prostředí navazuje na zkušenosti dětí s kostkami, zasahuje do aritmetiky a silně přispívá k rozvoji prostorové představivosti.
Děti nejdříve staví podle fantazie hradby, domy, ohrady, schody, věže, …
Zkušenosti rukou pomáhají rozvíjet prostorovou představivost dítěte. Rodič může pomáhat dítěti tím, že o jeho stavby jeví zájem a v komunikaci a komentářích činností upřesňuje jeho slovník. Dítě mluví o rohu krychle a my, aniž bychom dítě opravovali, používáme termín vrchol. Dítě řekne: „Tady to položím na toto.“ My můžeme jeho činnost komentovat: „Vidím, že jsi přiložil(a) stěnu na stěnu.“ Již nyní se také rozvíjí i argumentační schopnosti dětí. Jazyk, který dítě používá k popisu stavby, odráží jeho vlastní zkušenost a představy, proto dítě vysvětluje a obhajuje své pojmenování a vyjasňuje si popisy druhých dětí. Dítě rozvíjí své komunikační dovednosti v zájmu dorozumět se.
Z různých staveb, které děti tvoří, se omezíme na ty, které vznikly přikládáním stejně velkých krychlí vždy celou stěnou na celou stěnu. Nazveme je krychlové stavby. Stavba na obrázku tedy v našem smyslu krychlovou stavbou není, neboť dolní stěna modré krychle se s horní stěnou červené i bílé krychle překrývá jen částečně.
Od volné tvorby přecházíme ke kopírování. Děti s radostí a spontánně kopírují stavbu kamaráda. Často dochází mezi dětmi ke spolupráci a komunikacio tom, kam kterou kostičku přiložit. Je patrné, že pohled dítěte na stavbu je jižhlubší, všímá si detailů, např. počtu krychlí, jejich uspořádání, počtu podlažíapod. Zde se začínají rodit budoucí pojmy jako objem, výška tělesa, povrch, …
Hra na schovávanou rozvíjí krátkodobou prostorovou paměť a připravuje budoucí pojem shodnost těles. Krychlová stavba je někde ukryta. Dítě ji najde, zapamatuje si ji a postaví u sebe na koberci. Pak se schovaná stavba „přijde podívat“ na své dvojče.
Reakce dětí při porovnávání staveb ať již shodných, nebo zrcadlově souměrných, nebo jinak pozměněných bývají spontánní, radostné a nabyté diskusemi.
Úloha 1: Stavbu na v obrázku a) nazveme 4stupňové schodiště. Postav ji. Kolik krychlí na stavbu potřebuješ? Kterých je více, modrých nebo červených?
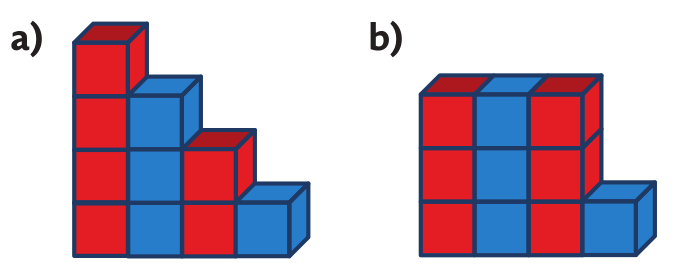
Mnoho dětí počítá po jedné. Objevují se i řešení 1 + 2 + 3 + 4 = 10, nebo: modré 1 + 3 a červené 2 + 4, celkem 10. Dítě, které upozorní na to, že tam mohou být i krychle schované, které nejsou na obrázku vidět, má vyspělé geometrické myšlení – schopnost v mysli pracovat s objekty, které v daný okamžik nevnímá zrakem. Děti také získávají zkušenost s lichými (modré) a sudými (červené) čísly a s rytmem.
Otázku: „Kterých krychlí je ve schodišti více?“ vyřešila jedna dívka tak, že přemístila nejvyšší červenou krychli a vytvořila stavbu jako na obrázku b). Bez počítání odpověděla, že červených krychlí je o 2 více. Vidíme, že prostor pro různé argumentace dětí je překvapivě velký.
Další úlohou podpoříme vnímání rytmu a posloupnosti čísel.
Úloha 2: Přidej jednu věž a vytvoř 5stupňové (6stupňové, 7stupňové) schodiště. Jak může dítě postupovat, má-li před sebou tento úkol? Některé děti dodrží rytmus barev a přistaví věž z pěti modrých krychlí a pak odpoví, jiné dříve odpoví, než postaví, některé vůbec nepostaví a řeší úlohu jen v představách.
Následující úlohou rozvíjíme kombinatorické myšlení.
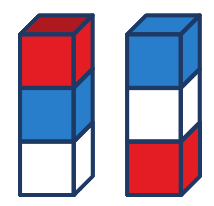
Úloha 3: Na obrázku jsou dvě různé věže ze tří krychlí – červené, modré a bílé. Kolik dalších různých věží z těchto tří krychlí můžeš postavit?
Úloha 4: Obyvatelé planety Krychlov žijí v krychlových stavbách postavených právě ze čtyř krychlí. Kolik nejvíce může být v Krychlově domů, když žádné dva nejsou stejné?
Úloha propojuje geometrii a kombinatoriku a při nedostatku krychlí vyvolává potřebu nějakého záznamu. Obvykle děti diskutují o tom, které stavby jsou stejné (shodné) a zda jsou například dvě stavby na obrázku stejné, nebo různé. Radka tvrdí, že jsou stejné, protože když se jedna z nich podívá do zrcadla, vidí se, jako by byla ta druhá. Šimon oponuje. Říká, že levá bota je jiná než pravá bota. Konečné rozhodnutí necháme na dětech. Někdy na druhém stupni dojdou k tomu, že jsou to nepřímo shodná tělesa.
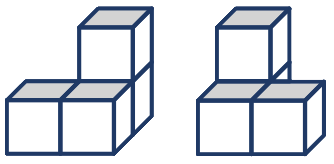
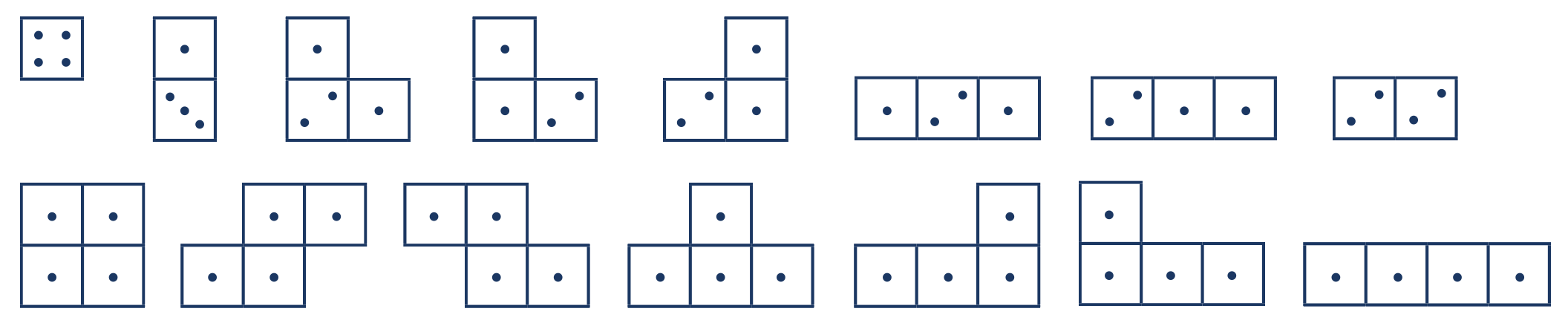
Návrhy dětí na záznamy staveb se postupně vyvíjí s cílem, aby všechny děti záznamu rozuměly a uměly jej vytvořit. Po čase se objeví záznam, který je pro všechny přijatelný. Stavbu znázorníme takto: Nakreslíme, jak ji vidíme shora, a počtem puntíků v jednom čtverci vyjádříme počet krychlí nad sebou. Dostáváme plán krychlové stavby. Na obrázku je plán levé stavby z obrázku u úlohy 4.

Úloha 3: Všech různých věží z daných tří krychlí je 6.
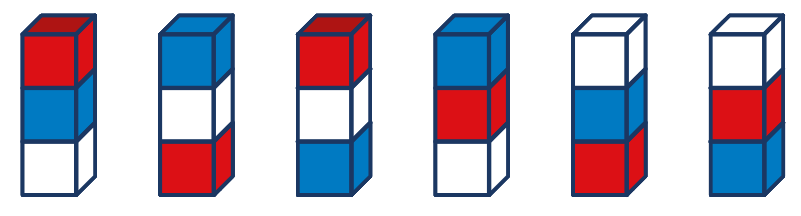
Úloha 4: V Krychlově může být nejvíce 15 různých staveb. Nejsou zobrazeny pootočené stavby.
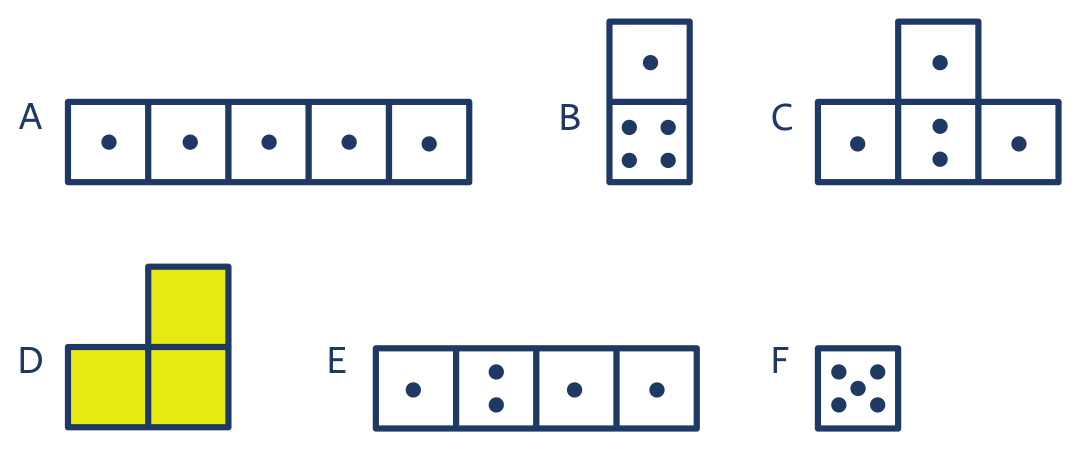
Úloha 5: Gábina postavila z krychlí „vláček“ (obr. A). Přeložila jednu krychli na jiné místo a novou stavbu zapsala plánem. Pak přeložila další krychli a vzniklou stavbu opět zapsala plánem. To opakovala ještě třikrát. Nakonec před ní stála věž (obr. F). Plány staveb, které Gábina zapsala, jsou na obrázcích A, B, C, D, E, F, ale v jiném pořadí. Navíc z plánu D jsou vymazány tečky. Najdi pořadí plánů a doplň tečky do plánu D.
Úloha 5:

Pracujeme s objemem krychlových staveb a zkoumáme povrch. Jednotkou objemu je 1 krychle, jednotkou obsahu je 1 čtverec, který je stěnou krychle. Tak např. 4stupňové schodiště z úlohy 1 má objem 10 krychlí a povrch 36 čtverců.
Úloha 6: Jaký největší a jaký nejmenší povrch má krychlová stavba s objemem:
a) 4 krychle
b) 8 krychlí
c) 27 krychlí?
Úloha 6: Představme si, jak stavba vzniká přidáváním jedné krychle. Povrch bude největší, pokud každou při- danou krychli „přilepíme“ pouze jednou stěnou k tomu, co už bylo postaveno. Může tak vzniknout mnoho rozmanitých staveb, z nichž nejjednodušší pro představu je „věž“ a) 4 × 1 × 1, b) 8 × 1 × 1, c) 27 × 1 × 1. Jejich povrch je tvořen a) 18, b) 36, c) 110 stěnami krychlí. Nejmenší povrch má a) hranol 2 × 2 × 1, b) krychle 2 × 2 × 2, c) krychle 3 × 3 × 3. Jejich povrch je tvořen a) 16, b) 24, c) 54 stěnami krychlí.