Prostředí:

Prostředí:
Od jednoduchých zákonitostí k rovnicím a posloupnostem
Pavučiny jsou strukturální prostředí. Děti zde pracují s čísly v abstraktní podobě a řešením promyšlených sérií úloh objevují zákonitosti. Získávají zkušenosti vztahující se k rovnicím a k porozumění obtížnějším pojmům aritmetiky, jakými jsou aritmetická posloupnost a aritmetická řada.
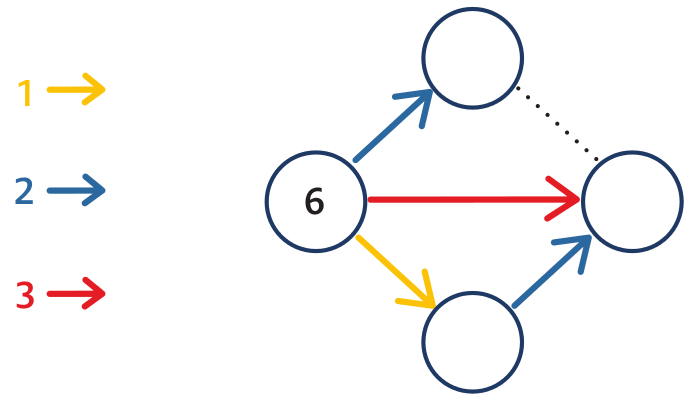
Vidíme zde čtyři kolečka, v jednom je číslo 6 a do tří prázdných koleček máme čísla dopsat. Dále je zde 1 žlutá šipka, 2 modré a 1 červená a 1 vytečkovaná úsečka. Žlutá šipka značí „přičítej 1“. Do dolního kolečka tedy dopíšeme 7 (6 + 1). Modrá šipka říká „přičítej 2“. Do horního kolečka napíšeme 8 (6 + 2) a do pravého 9 (7 + 2). Červená šipka přičítá 3. Jen zkontrolujeme: 6 + 3 = 9. Tečkovaná úsečka spojuje čísla 8 a 9. Doplníme tedy žlutou šipku od 8 k 9.
Úloha 1: Doplň čísla a šipky do pavučin.
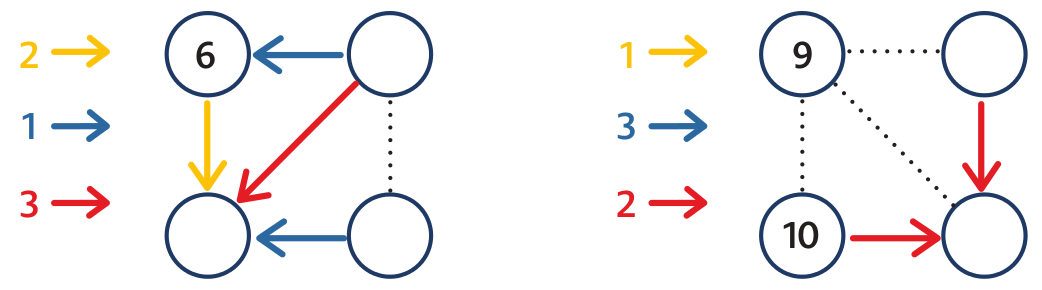
První pavučina: Z pravého kolečka vede modrá šipka, která přičítá 1, do čísla 6. Hledáme tedy číslo, ke kterému když přičteme 1, dostaneme 6. Doplníme 5. Některé dítě odčítá (5 = 6 – 1). Nechme každému dítěti jeho vlastní postup. V dolním levém kolečku musí být 8 (6 + 2 nebo 5 + 3). V dolním pravém kolečku je 7 (protože 7 + 1 = 8, nebo 7 = 8 – 1) a doplníme žlutou šipku směřující dolů od 5 k 7.
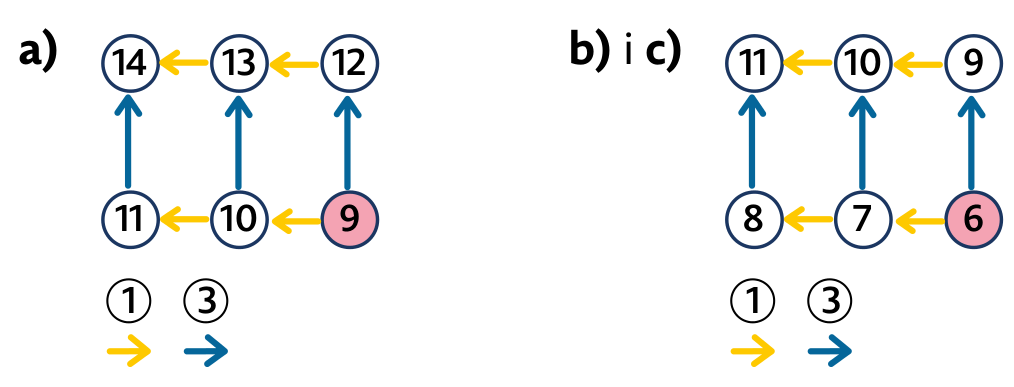
Po vyřešení druhé pavučiny si některé děti všimnou, že do pravého dolního čísla 12 míří dvě červené šipky a obě začínají ve stejném čísle, v 10. Je to první zkušenost se zákonitostí, že když ze dvou kroužků vedou dvě stejně barevné šipky do jednoho kroužku, tak v těch dvou kroužcích musí být stejná čísla. Chceme-li, aby žáci objevili, že je to zákonitost, které lze využít při řešení některých úloh, připravíme jim sérii dalších pavučin – první a třetí pavučina v úloze 2.
Úloha 2: Doplň čísla do pavučin a k šipkám.
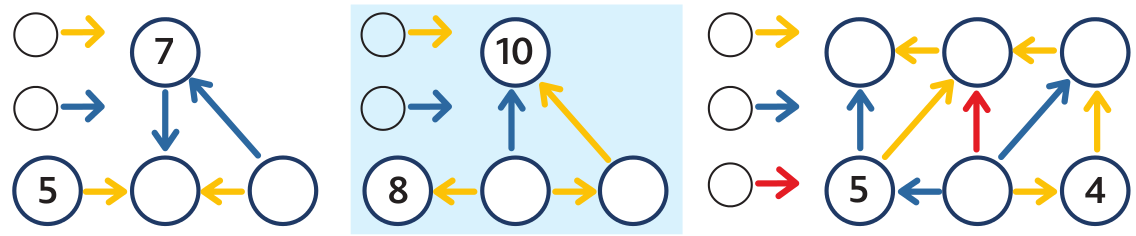
První pavučina: Žák řeší pokusem–omylem a volí například 6 do prostředního kroužku. Brzy ale zjistí, že pavučina nefunguje, že modré šipky nepřičítají stejné číslo. Tedy zvolí další číslo, například 8. Opět pavučina nefunguje. Když zvolí doprostřed číslo 9, pavučinu dopočítá, vpravo je 5, a zjistí, že již funguje.
Když si dítě zákonitosti nevšimne ani po několika dalších úlohách, které mu nabídneme, vůbec to nevadí, dítě pracovalo, hodně počítalo a získávalo vhled do situace. Třeba na ni přijde později nebo mu ji napoví jiný žák. Jen se zdržme zákonitost sami prozradit. Když vidíme, že dítě uvedenou zákonitost již využívá k řešení, zeptáme se, co kdybychom v zadání změnili 5 na 3, nebo 1. Když dítě odpoví, že tam budou vždycky stejná čísla, přivedli jsme jej ke skutečnému objevu zákonitosti, která je výše popsána.
(Matematicky bychom ji mohli popsat takto: Jestliže pro reálná čísla x, y, a platí, že x + a = y + a, pak x = y).
Dále ukážeme, jak děti získávají zkušenosti s řešením jednoduchých rovnic a s aritmetickou posloupností.
Úloha 3: Doplň.
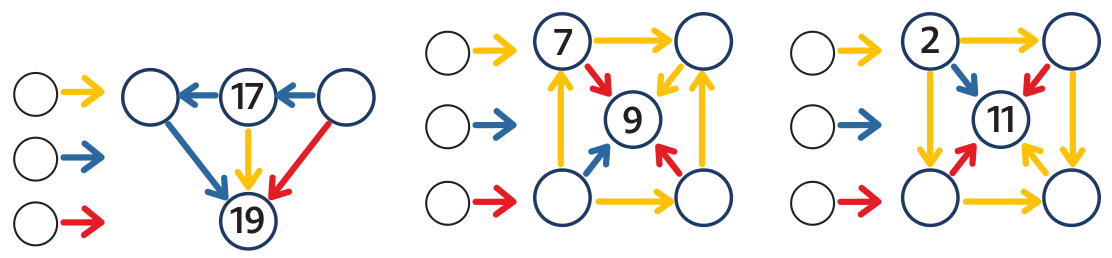
V první pavučině vidíme sérii tří modrých šipek. Dítě vidí, že z čísla 17 se dostane dvěma modrými šipkami do 19. Situace je tak výmluvná, že je hned vidět, že vlevo je číslo 18. Modrá šipka tedy přičítá 1 a v pravém kroužku je 16. (Zapišme to jazykem matematiky: 17 + 2m = 19, tedy m = 1. Číslo m je to, které přičítá modrá šipka. Dále můžeme říci, že čísla 16, 17, 18 a 19 jsou čtyři po sobě jdoucí členy aritmetické posloupnosti, která roste po 1.)
Ve druhé pavučině je situace obdobná, jen trochu méně přehledná.
Ve třetí pavučině jsou třemi žlutými šipkami spojena 4 čísla posloupnosti: 2, ?, ?, 11. Žák si ale říká: „Z 2 do 11 se dostanu třemi žlutými šipkami. Ty přičtou dohromady 9, tedy jedna žlutá šipka musí přičíst 3.“ V pavučinách si děti snadno zkontrolují, zda pavučina „funguje“ a případně si samy mohou najít chybu.
Úloha 1:
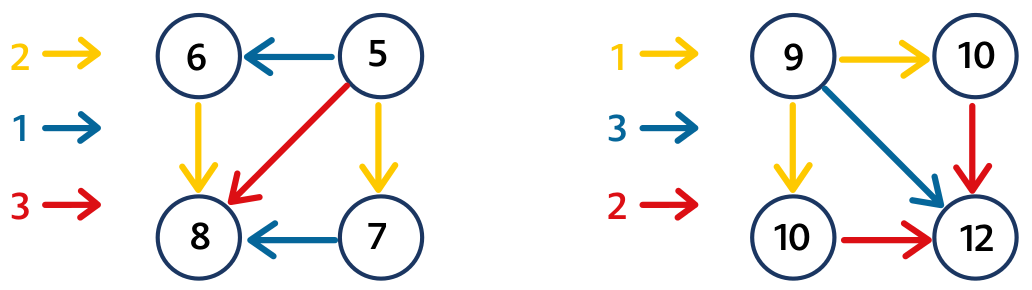
Úloha 2:

Úloha 3:

Úloha 4: Doplň pavučiny, když víš, že a) nejmenší číslo je 5; b) největší číslo je 100; c) součet nejmenšího a největšího je 11; d) součet všech pěti čísel je 15.
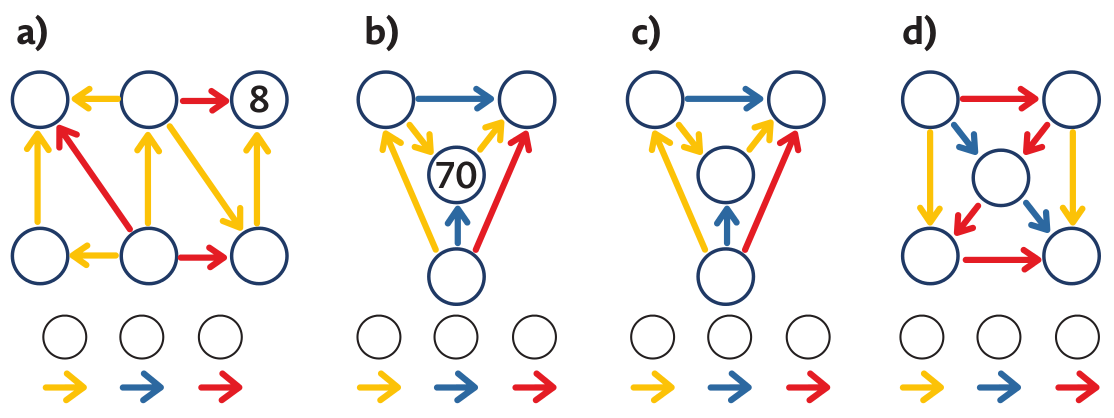
V úloze a) děti uvažují o pozici nejmenšího čísla pavučiny a argumentují, proč nejmenší číslo je zrovna to, ze kterého všechny šipky vycházejí. Obdobně pro největší číslo v úloze b).
Úlohy c) a d) jsou již obtížnější a vyžadují mnohé počítání. Matematik by využil vztahů čísel v aritmetické posloupnosti a řešení by vedlo k rovnici o dvou neznámých. V c) je to 2x + 3y = 11, v d) 5x + 10y = 15, kde x je dolní, resp. pravé dolní číslo v pavučině a číslo y přičítá žlutá, resp. červená šipka. Rovnice v c) má 2 řešení v přirozených číslech a rovnice v d) jedno řešení.
Úloha 4:

Úlohou 5 otevíráme dokořán dveře rovnicím.,
Úloha 5: Zvol růžové číslo tak, aby součet
a) tří dolních čísel byl 30;
b) tří horních čísel byl 30;
c) všech šesti čísel byl 51.
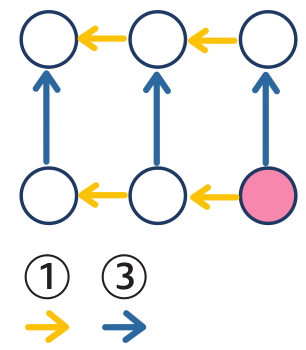
Děti, které již umí pracovat s neznámým číslem pomocí x, si doplní x do růžového kolečka a dále dopíší x + 1 a x + 2, a nahoru x + 3, x + 4 a x + 5.
Samozřejmě děti nenutíme do použití písmen. Písmena začnou používat, až uvidí, že jim přinášejí zjednodušení.
Úloha 5: