
Prostředí:

Prostředí:
Od čísel k algebraickým výrazům.
Jazyk písmen je devíza především druhého stupně. Na prvním stupni se žáci na použití písmen v matematice pečlivě připravují. Např. již v úlohách v prvním ročníku se vyskytuje „klasická“ úloha 2 + 
Ale s takovými zápisy nespěcháme, ty přijdou později, až děti budou mít více zkušeností a na písmena budou připraveny. Úlohy, jejichž řešením je vytvářena potřeba popsat obecnou zákonitost, nebo i jednoduchý vztah, účinně vedou žáky do algebry. Např. při objevování vzorce pro obvod čtverce děti manipulacemi s dřívky řeší úlohy s konkrétními čísly.
Pro stranu čtverce tvořenou jedním dřívkem vyjde obvod čtyři dřívka. Pro stranu se dvěma dřívky vyjde obvod osm dřívek atd. Děti začnou postupně popisovat obecnější zákonitosti. Od „sečtu délky stran,“ k známému a + a + a + a, určitě zazní i „čtyřikrát vynásobím stranu,“ neboli 4 · a. Ve třídách se objevily i další možné (a správné) zápisy pro obvod čtverce. Potřeba zkracovat si zápis vede postupně k používání písmen ve významu proměnné. Některé úlohy přímo vybízejí, aby se po sérii řešení s čísly našel obecně platný vztah.
Děti samy často některá zadání vedou k zobecnění, když zaznívá: „A jak to bude vypadat dál, a jak někde v nekonečnu?“
Úlohy, které děti řeší, jsou často tvořeny tak, že od konkrétních čísel a modelů děti objevují zákonitost obecnou.
Úloha 1: První čtverec na obrázku má délku strany 1 dřívko a je složen ze 4 dřívek. Druhý čtverec o délce strany 2 dřívka je poskládán z 12 dřívek. Třetí čtverec na obrázku má délku strany 3 dřívka a je poskládán z 24 dřívek.
Určete, z kolika dřívek je poskládán podobně vytvořený čtverec s délkou strany 4, 5, 10, 100 dřívek.
Najděte obecný vztah.
V zadání prvního součtového trojúhelníku je místo písmene
hvězdička. Děti mají s hvězdičkou místo číslice dostatek zkušeností – například právě při řešení úloh z prostředí Hvězdičkogramy. To může být i důvodem, proč zatím některé děti upřednostňují hvězdičku před písmenem. Následující úloha umožní dětem, aby hvězdičku nebo číslo považovaly pouze za jiný způsob zápisu, který zde neovlivní řešení prvního a druhého trojúhelníku.
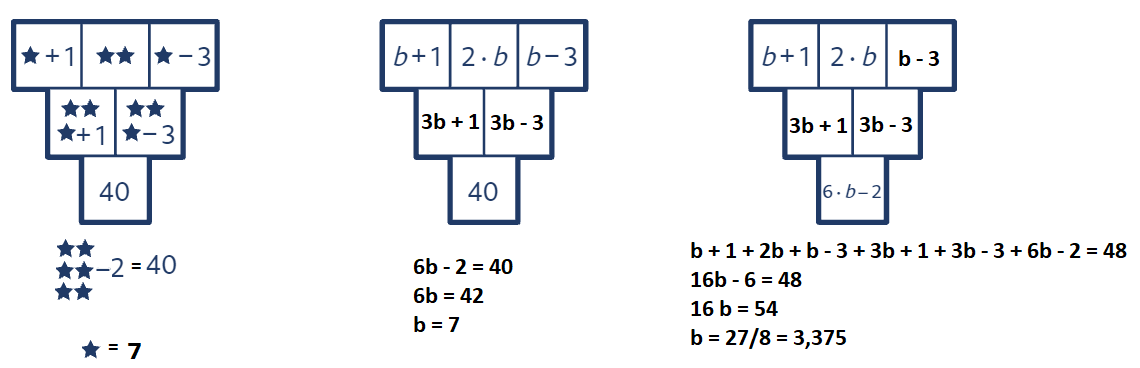
Úloha 2: Součtové trojúhelníky vyřešte. Ve třetím trojúhelníku
najděte b tak, aby součet všech šesti čísel trojúhelníku byl 48.
Úloha 1:
Úlohu lze zobecnit různě. Např. se budou evidovat zvlášť svislá a vodorovná dřívka. Svislých dřívek je vždy n · (n + 1), kde n je délka strany čtverce. To samé platí i pro vodorovné dřívka. Takže dohromady vždy bude 2 · n · (n + 1) dřívek.
Čtverec s délkou strany 4 dřívka: 40 dřívek, čtverec s délkou strany 5 dřívek: 60 dřívek, čtverec s délkou strany 10 dřívek: 220 dřívek, čtverec s délkou strany 100 dřívek: 20 200 dřívek.
Úloha 2:
Díky sadě dlaždic, kterou má k dispozici každé dítě, mají všichni možnost vytvořit si konkrétní představu, co znamenají jednotlivá písmena. To, že s dlaždicemi manipulují, jim výrazně napomáhá k porozumění. Později jim dvoubarevné dlaždice umožní řešit i úlohy s rozdíly. Postupně si odvozují, jakým způsobem násobíme dvojčlen dvojčlenem, a seznamují se s algebraickými vzorci.
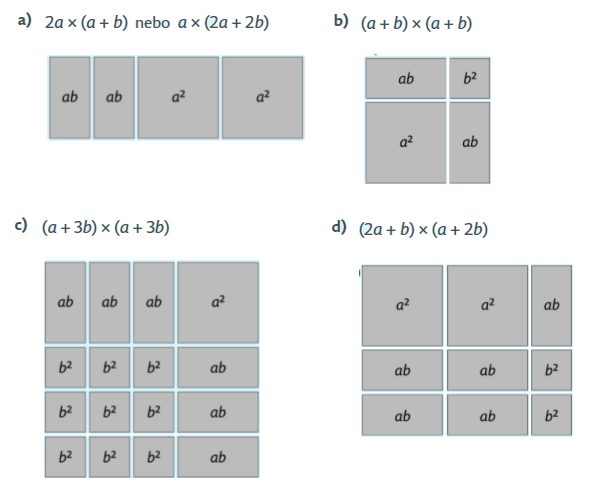
Úloha 3: Z uvedených dlaždic poskládejte pravoúhelník (obdélník
nebo čtverec). Pomocí písmen a, b vyjádřete jeho obsah.
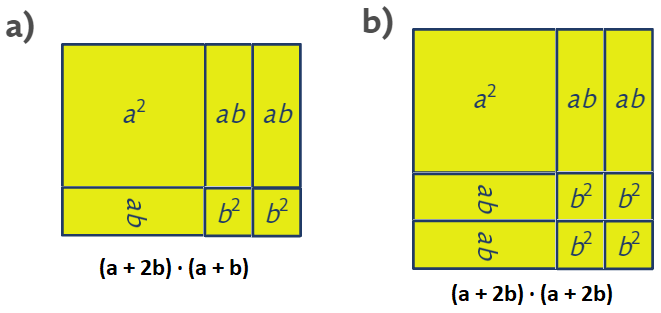
Úloha 4: Pomocí vhodných dlaždic poskládejte
pravoúhelník s obsahem:
Pomocí písmen a, b vyjádřete délky stran.
Jedním z cílů této úlohy je, aby děti sdělovaly svoje strategie řešení, aby je navzájem porovnávaly a postupně docházely k zobecňování (někdo doplňuje na čtverec, někdo „hledá systém“ – vypozoruje ho a ověří apod.). Při porovnávání svých řešení začínají upravovat výrazy s proměnnou.
Úloha 5: Na obrázku je záhon ve tvaru písmene L a kolem něj
zahradník pokládá kachlíky.

Kolik kachlíků je potřeba na záhon tvaru L o velikosti:
Úloha 6: Na obrázku je 2-hvězda a 3-hvězda.
Zjistěte, kolik koleček je potřeba na postavení:
Opakovaně jsme zmiňovali, že děti používají různé řešitelské strategie. Pro zajímavost přikládám Verčin způsob řešení, které považuji za originální, zatím s ním nikdo jiný nepřišel. Verča svůj objev okomentovala slovy: „Podívala jsem se na to a prostě jsem to viděla.“
Úloha 3:
Úloha 4:
Úloha 5:
Úloha 6: