Prostředí:
Parkety
Parkety jsou geometrickým manipulativním prostředím.
Postupně jsou zaváděny „parkety“ složené ze čtverců, tzv.
čtvercová polymina.
Prostředí:
Činností získáváme zkušenosti s rovinnou geometrií.
Parkety jsou geometrickým manipulativním prostředím.
Postupně jsou zaváděny „parkety“ složené ze čtverců, tzv.
čtvercová polymina.
K pokrývání podlahy můžeme použít 9 druhů parket nakreslených na obrázku:
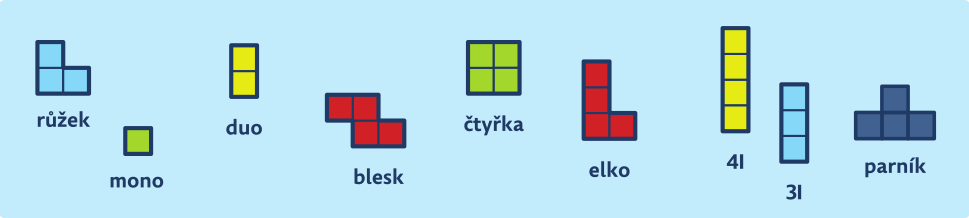
Sami žáci se mohou domluvit, jak jednotlivé parkety pojmenují. Později se názvy sjednotí, aby nedocházelo k nedorozumění při řešení úloh. Důležité je, aby každý žák měl možnost manipulovat s pomůckami. Jsou dostupné dřevěné, magnetické, nebo je učitel sám vyrobí z kartonu nebo zalaminovaného papíru. Při řešení úloh v prostředí Parkety děti získávají zkušenosti s rovinnou geometrií: geometrickými tvary a jejich skládáním, s obsahem i obvodem útvarů, se shodnými zobrazeními (osová souměrnost, středová souměrnost, otočení). Další oblastí bohatě se rozvíjející v prostředí je kombinatorika.
K zavedení prostředí v 1. ročníku slouží následující úloha:
Úloha 1: Parketami mono a růžek pokryj podlahu. Najdi více řešení.
V ní se žáci seznamují s prvními dvěma druhy parket:
mono 
a růžek 
.
Zde spontánně proběhne diskuze o tom, zda úloha má 4 nebo 1 řešení (protože je pouze 1 řešení, které otáčíme).
Úloha 2: Pokryj parketami podlahu. Najdi různá řešení.
Žáci zjistí, že jim jedna parketa duo nebo dvě parkety mono schází.
Tím získávají zkušenosti s obsahem. Učitel je poté vyzve, aby si jednu parketu duo doplnili a ptá se: „Kde může a kde nemůže být ve čtverci umístěno mono, aby čtverec šel postavit?“
Ještě v 1. ročníku přijdou úlohy s podmínkou. Jedna z takových se týká rozdílů mezi slovy dotýkat se (mají společný pouze vrchol) a sousedit (mají alespoň jednu stranu společnou). Je nutné ve třídě toto vyjasnit diskuzí.
Úloha 3: Parketami pokryj podlahu.
Další úloha cílí na obsah obdélníku 4 × 3 (12 čtverečků). Děti zjišťují, že musí použít buď 3 parkety se 4 čtverečky, nebo 4 parkety s 3 čtverečky. Hledáním takových řešení rozvíjejí i kombinatorické myšlení.
Úloha 4: Vyber parkety a pokryj podlahu tvaru obdélník 4 × 3.
Hledej více řešení.
Další úloha připravuje osovou souměrnost, nejdříve se svislou
osou, později i s osou vodorovnou.
Úloha 5: Překresli. Souměrně pokryj parketami.
Úloha 1:
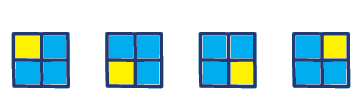
Úloha 2:
Mono může být na těchto polích:
Úloha 3:
Uvádíme jedno možné řešení.
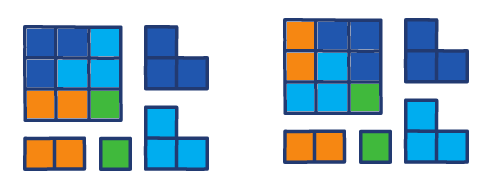
Úloha 4:
Uvádíme pouze některá řešení.
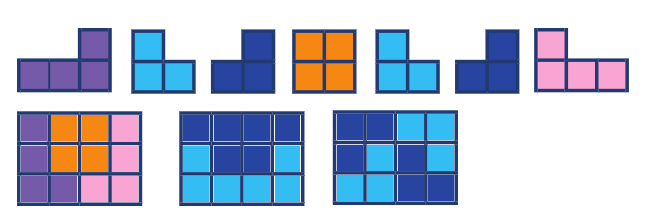
Úloha 5:
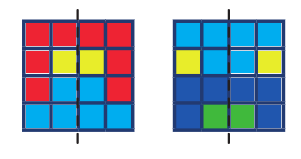
Úloha 6: Obdélník 7 × 2 pokryjte pouze parketami
a 
. Kolik kterých parket použijete? Hledejte více řešení co do počtu použitých parket.
Úloha 7: Stejnou úlohu řešte pro dvojici parket:
Úloha 8: Obdélník 20 × 2 pokryjte pouze dvojicí parket:
Úloha 6:
Existují tři řešení. Buď použijeme čtyři parkety 3I a jedno duo (D), nebo dvě parkety 3I a čtyři D, nebo pouze sedm D.
Úloha 7:
a) čtyři řešení (Duo, Čtyřka) = (1, 3), (3, 2), (5, 1), (7, 0)
b) tři řešení (Růžek, Duo) = (0, 7), (2, 4), (4, 1)
c) čtyři řešení (Mono, Blesk) = (2, 3), (6, 2), (10, 1), (14, 0)
d) jediné řešení (Růžek, Blesk) = (2, 2)
e) jediné řešení (Růžek, Elko) = (2, 2)
Úloha 8:
Pomalejší žáci se spokojí s nalezením jediného řešení.
Rychlejší žáci u úlohy a) zjistí, že čtyřek může být od 10 do 0, tedy úloha má 11 řešení. Tím vlastně řeší diofantickou rovnici 4 · Č + 2 · D = 40, tj. 2 · Č + D = 20, kde Č značí počet čtyřek a D počet duí. Podobně je tomu u dalších úloh.
Když zadáme expertům stejnou úlohu pro obdélník 50 × 2, vyzdvihneme tím význam uchopení problému pomocí diofantické rovnice. Navíc u úloh d) a e), jak v originálním, tak expertním zadání, dojde k překvapení: ne všechna řešení příslušné diofantické rovnice jsou v praxi realizovatelná. Diofantická rovnice nám tedy poskytuje jen nutnou, ne však zcela postačující podmínku k realizaci.
Výsledky pro obdélník 20 × 2:
U úloh a) a b) jsou všechna řešení (včetně těch, která využívají pouze jeden typ parket) příslušné rovnice realizovatelná.
a) 4 · Č + 2 · D = 40, tj. 2 · Č + D = 20, (Č, D) = (0, 20), (1, 18), …, (10, 0); 11 řešení.
b) 3 · R + 2 · D = 40, (R,D) = (0, 20), (2, 17), …, (12, 2); celkem 7 řešení.
c) 4 · B + M = 40, (B, M) = (0, 40), (1, 36), …, (9, 4); celkem 10 řešení.
d) 4 · B + 3 · R = 40, (B, R) = (1, 12), (4, 8), (7, 4), (10, 0); avšak poslední možnost není realizovatelná, takže existují jen 3 řešení.
e) 4 · L + 3 · R = 40, (L, R) = (1, 12), (4, 8), (7, 4), (10, 0), avšak jen možnosti (4, 8) a (10, 0) jsou realizovatelné, takže existují jen 2 řešení.
Parkety lze využít na důkazové úlohy. Ty požadují po žácích najít řešení nebo dokázat, že řešení neexistuje. To zlepšuje jejich argumentační a vyjadřovací schopnosti.
Úloha 9:
a sedmi 
pokryjte šachovnici 4 × 4,ze které je vyříznuto rohové pole..
Úloha 10: Ze šachovnice 8 × 8 jsou vyříznuta dvě protilehlá pole.
Pokryjte ji pouze parketami duo 
.
Úloha 9:
Klíčovou myšlenkou je to, že parketa duo vždy padne na jedno bílé a jedno modré pole. Protože jedno modré pole chybí, musí být nutně parketa mono na libovolném bílém poli.
Úloha 10:
Řešení neexistuje. Zdůvodnění vyplývá z úlohy 9. Parketa duo vždy pokrývá jedno bílé a jedno modré pole. Ale ze šachovnice jsou vyseknuta dvě modrá pole.