
Prostředí:

Prostředí:
Toto prostředí seznamuje žáky s velmi důležitým jevem periodicity (tedy pravidelnost při opakování). V matematice je porozumění tomuto jevu velmi důležité, protože se objevuje v mnoha oblastech (periodický rozvoj číslic za desetinnou čárkou, periodické funkce sinus a kosinus, geometrické objekty fraktály atd.). Kromě toho přispívají úlohy z tohoto prostředí také porozumění číselným soustavám o jiném základu než 10 a k modulární aritmetice.
S jevem periodicity mají žáci zkušenosti již od 1. třídy, kdy řeší úlohy na určování času na dvanáctihodinovém ciferníku (viz prostředí Ciferník). Když řeknu, že jsem z domova odešel ve 12 hodin a vrátil jsem se za hodinu, ručička bude na ciferníku ukazovat na číslo 1. Je tomu tak proto, že struktura na ciferníku je zacyklená a opakuje se. Na klasické číselné ose, tedy na přímce, by za číslem 12 bylo číslo 13, protože tato struktura je lineární. Tento rozdíl v obou strukturách je klíčový a vede k velmi zajímavým vlastnostem.
Úloha 1:

Odhalení pravidla, podle kterého je posloupnost vytvořená, není složité. Pokud by ho přeci jen žáci neodhalili, vysvětluje ho modrý rámeček níže. Důležité je, aby měli žáci k dispozici ciferník, s jehož pomocí lze řešení úlohy dobře vizualizovat. Seznamují se i s jiným než dvanáctihodinovým ciferníkem.

Úloha 2:
Následující úloha může vést k zajímavému zamyšlení. Když přičítám 2, projdu polovinu všech čísel ciferníku. Když přičítám 4, projdu jen tři čísla na ciferníku. Které číslo mám přičítat, abych prošel co nejvíce nebo co nejméně čísel ciferníku? A na čem to záleží? Tyto úvahy úzce souvisí s dělitelností čísel. Žáci budou mít ještě dostatek příležitostí na jejich zodpovězení, klidně až na 2. stupni.

Úloha 3:
Následující úloha je oproti dvěma předcházejícím sémantická. To znamená, že čísla, která se v úloze vyskytují, mají nějaký reálný význam. Zde se jedná o časové údaje a frekvenci, jak často má trpaslík brát léky. Žáci pracují s ciferníkem, který má 7 hodin.

Úloha 2:
a) 2, 4, 6, 8, 10, 12, 14, 2
b) 3, 7, 11, 15, 3
c) 1, 6, 11, 16, 4, 9, 14, 2, 7, 12, 17, 5, 10, 15, 3, 8, 13, 1
Úloha 3:
a) ve 2 hodiny
b) ve 3, 2, 1, 7, 6, 5, 4, 3, … hodiny
Úloha 4:
V úloze pracujeme s posloupností, kterou lze vizualizovat na osmihodinovém ciferníku. Pokud žáci potřebují obrázek, mohou si ho nakreslit nebo jim ho nabídne učitel. Úloha dále rozvíjí myšlenku, kterou jsme nastínili v komentáři k úloze 2. Žáci jsou vyzváni k tomu, aby si všímali, ve kterých posloupnostech se objeví všechna čísla od 1 do 8. Mohou pak dle toho vyslovovat hypotézy o tom, proč tomu tak je. Tyto hypotézy se dají zkoumat i na jiných cifernících.

Úloha 5:
Posloupnosti můžeme zapisovat i římskými číslicemi.

Úloha 6:
Dalším typem úlohy je hledání chyb v již napsaných posloupnostech. Chybu lze opravit mnoha způsoby.

Úloha 7:
Jev periodicity dále rozvíjíme nejen na ciferníku, ale také na směrové růžici (což můžeme ale také chápat jako čtyřhodinový ciferník). Je důležité, aby žáci pochopili proces, kterým se čísla namotávají na růžici. Proto necháme žáky pokračovat tak dlouho, dokud to budou potřebovat. Poté je můžeme vyzvat, aby pokračovali v posloupnosti u jedné světové strany a aby popsali, jak vzniká (přičítáním čísla 4). Dalším krokem je zjišťování, kam které číslo padne. Díky tomu postupně žáci přijdou na to, že u severu jsou násobky 4, u východu násobky 4 zvětšené o 1, u jihu násobky 4 zvětšené o 2 a u západu násobky 4 zvětšené o 3. Všechny tyto objevy ale vyžadují hodně času, experimentování a nasbíraných zkušeností.

Úloha 8:

Úloha 9:
V úloze 9 a 10 mají žáci odhalit, že řešení úloh na růžici souvisí s násobky 4, respektive se zbytkem po dělení čísla 4. Tento princip je základem oblasti, která se nazývá modulární aritmetika. Jedná se o zajímavou matematickou strukturu, která funguje jinak než klasická lineární číselná osa.
Zjisti, ke kterému směru naší směrové růžice padne číslo: 13, 26, 44, 59, 85, 102, 127, 148, 294, 656, 894, 999, 2 421, 7 836.
Úloha 10:
Rozděl daná čísla do skupin podle zbytku při dělení číslem 4: 13, 26, 44, 59, 85, 102, 127, 148, 294, 656, 894, 999, 2 421, 7 836.
Úloha 4:

Všechna čísla od 1 do 8 se objeví v úlohách b) a d), kde jsou skoky mezi jednotlivými čísly 3 a 5. Jak to souvisí s 8 ze zadání?
Úloha 5:
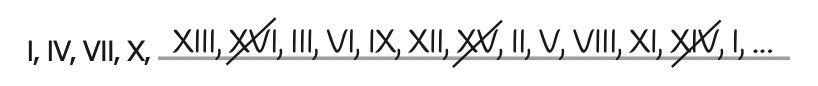
Úloha 6:

Úloha 7:

Úloha 9:
Sever: 44, 148, 656, 7 836;
Východ: 13, 85, 2421;
Jih: 26, 102, 294, 894;
Západ: 59, 127, 999.
Úloha 10:
viz předchozí úloha (sever → beze zbytku, východ → zbytek 1, jih → zbytek 2, západ → zbytek 3)