Procenta

Získávání zkušeností z běžného života – slevy, ankety, složení výrobků, …

Úvodní povídání o zkušenosti s procenty z každodenního života má význam jak pro žáky, tak pro učitele. Pro děti je to impulz motivační a pro učitele dobrý diagnostický nástroj poznat, kteří žáci ve třídě tento pojem ovládají. Jednou z takových aktivit je výzva, aby děti přinesly příklady slev z obchodů, kde byly nakupovat. Ve třídě pak děti počítají, zda obchod ceny určil správně.

Úlohy s procenty vyžadují někdy náročnější násobení nebo dělení a k tomu žáci využívají kalkulačku. Důležitější než operace písemného násobení nebo dělení bez kalkulačky je vhled do práce s procenty, desetinnými čísly a se zaokrouhlováním.

V praxi se ukázalo, že hodně žáků v začátcích využívá jinou strategii k řešení úloh s procenty než dospělí (přes 1 %). Žákovskou strategii si ukážeme na následující úloze:

Úloha: Učebnice stála 120 Kč. Urči, kolik korun činí 15% sleva z učebnice.

Dobře umí spočítat 50% slevu, 25% slevu a další „hezké“ slevy. Výpočet 15% slevy je ale obtížná úloha.

Dříve než se objeví přechod přes 1 %, žáci často využívají metodu „krájení“. 50 % rozdělí na 5 částí po 10 %. Jednu z těchto částí rozdělí na poloviny, tzn. 5 % a 5 %. Nakonec dají 10 % a 5 % dohromady a získají 15 %. V naší úloze 50 % je 60, 10 % je 12 a 5 % je 6. 10 % a 5 % dohromady je 18 Kč. Po dalších zkušenostech s podobnými úlohami se objeví i přechod přes 1 %.

Následující úloha s procenty vede k postupnému objevení vztahů mezi procentovou částí, počtem procent a základem. Vzorce žákům nedáváme, ale pokud si je objeví sami a mají potřebu je zapsat, je to v pořádku.

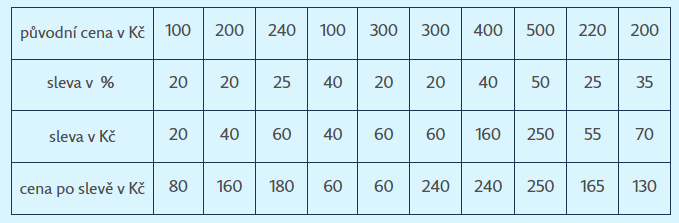
Úloha 1: Doplňte scházející data do tabulky:

Další úlohu řeší žáci v geometrickém kontextu. Úloha cílí na propojení procent a zlomků a jejich vzájemný převod.

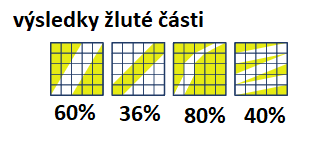
Úloha 2: Zjistěte, kolik procent čtverce je vybarveno a kolik procent zůstalo nevybarveno.

Žáci často využívají strategii skládání: spojení vybarvených částí do obdélníku nebo jiného, dobře známého útvaru.

Následující úloha je klasickým chytákem. Žáci bez hlubšího vhledu do procent okamžitě křičí: „To vyjde zase 3 200.“ Jiní spolužáci je ale posléze přesvědčí o jejich omylu.

Úloha 3: Letenka stála v lednu 3 200 Kč. V únoru byla její cena zvýšena o 25 %. V dubnu byla její cena snížena o 25 %. Kolik korun stála letenka v květnu?

Úloha 4: Ariana řešila mnoho úloh, ve kterých se letenka zdražovala o 50 %. Její původní cena je v prvním řádku tabulky. Doplňte druhý řádek.

Thuy k předchozí úloze řekla, že jí k výpočtu každého čísla stačí jediné násobení. Jak to Thuy dělá? Zvládnete to také?

Úloha 5: V únoru byla cena letenky zvýšena o 25 %. V dubnu byla
její cena zvýšena o 10 %. V květnu stála 6 600 Kč. Zjistěte, kolik stála letenka a) v březnu, b) v lednu.

Další úloha se zaměřuje na důležitou myšlenku.
Při řešení úlohy a) žáci okamžitě hlásí: „To je přeci jasné.“ Saúdská Arábie má více km2 lesů, proto je lesnatější. Vždy se ale nějaký žák, který oponuje: „No jo, ale tys nebral v úvahu velikost (rozlohu) obou zemí. S tím musíš počítat.“ Poté žáci začnou jednotlivé rozlohy vyhledávat a řešit úlohy. Takovými diskuzemi se kultivuje porozumění pojmům jako lesnatější, lidnatější atd.

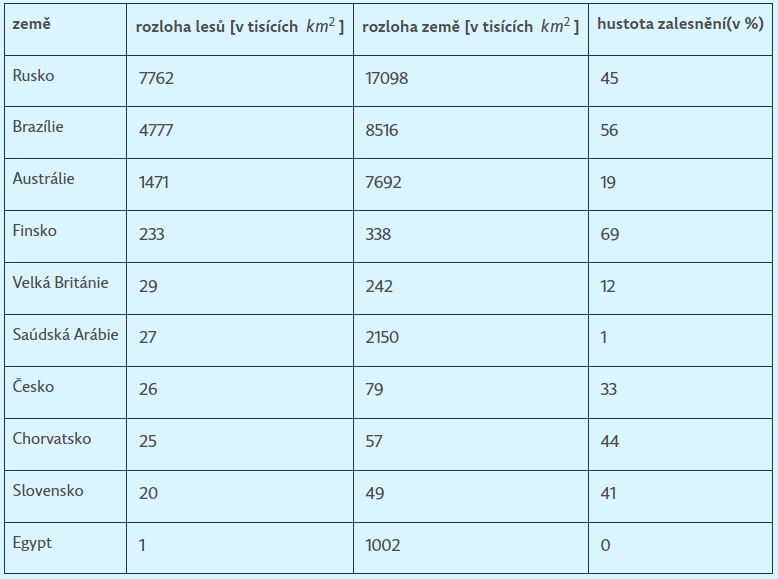
Úloha 6: V tabulce jsou rozlohy lesů vybraných zemí (data pochází
z roku 2011).
a) Je lesnatější Česko, nebo Saúdská Arábie?
b) Je lesnatější Slovensko, nebo Austrálie?
c) Jakou rozlohu lesů by musela mít Velká Británie, aby byla stejně
lesnatá jako Finsko?
d) Která z uvedených zemí je nejlesnatější a která nejméně lesnatá?

Následující dvě úlohy jsou z finanční gramotnosti. 

Jak zjistit, kde spořit a kde si naopak vybrat úvěr či půjčku? Jaký je rozdíl mezi složeným a jednoduchým úrokováním? Odhady, kolik uspoříme např. za 20 let s úrokovou sazbou 2 %, když do banky vložíme 100 000? To všechno jsou otázky, které přispívají k rozvoji finanční gramotnosti.

Úloha 7: Pan Novák si vložil kapitál 1 000 000 Kč do banky, ve které v prvním roce byla úroková sazba 2 % a ve druhém roce 3 %. Pan Procházka si vložil kapitál 1 000 000 Kč do jiné banky, kde v prvním roce byla úroková sazba 3 % a ve druhém roce 2 %. Kdo po dvou letech více vydělal?

Úloha 8: Paní Fialová si potřebuje půjčit 10 000 Kč na jeden rok. První banka nabízí úrok 2 % měsíčně – každý měsíc zvýší dlužnou částku o 2 %. Druhá banka nabízí úrok 25 % ročně – na konci roku zvýší dlužnou částku o 25 %. Paní Fialová celou dlužnou částku včetně úroků zaplatí po jednom roce. Která banka je pro ni výhodnější?