Prostředí:

Prostředí:
Z hlediska informatického se ve vývojovém diagram objevuje i práce s podmínkou → “Platí něco, pak něco vykonej, pokud to neplatí, vykonej něco jiného”.
Z hlediska matematiky se žáci seznamují s výroky, rozhodují o jejich pravdivosti. Důležitou součástí je i sběr dat, které vývojový diagram vydá a jejich vyhodnocení.
Úlohu je v začátcích dobré vizualizovat ve třídě, žáci si tak mohou jednotlivé kroky procesu projít za pomoci vlastního těla.
Úloha 1:
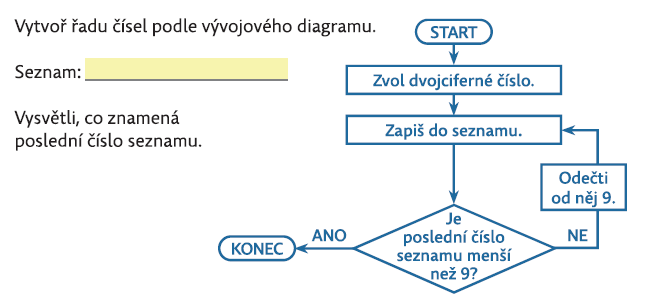
Vývojový diagram z úlohy popisuje přes opakované odčítání proces dělení číslem 9. Počet odečtení čísla 9 určuje neúplný podíl při dělení 9. Poslední číslo v seznamu dává zbytek po dělení.
Např. zvolím číslo 34.
Řešili jsme vlastně úlohu 34 : 9 = 3 (7). Neúplný podíl 3 ve výsledku odpovídá v našem diagram tomu, že jsme celkem třikrát odečetli 9, než jsme se dostali nakonec. Zbytek vyšel 7, což odpovídá poslednímu číslu v našem seznamu.
K úlohám s vývojovými diagramy se často take využívá náhoda – házení kostkou. Úlohy poté získají směr ke statistice, s žáky se dají řešit výzvy spadající do oblasti práce s daty (sběr dat, evidence dat, vyhodnocování dat,…).
Úloha 2:
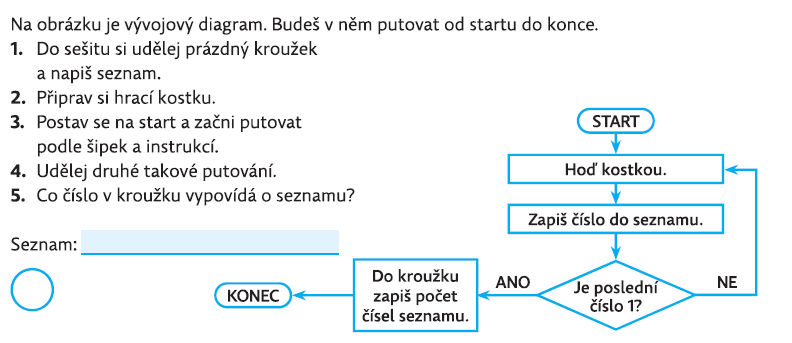
V této úloze se eviduje na konci procesu počet čísel v seznamu. Žáky vyzýváme k interpretaci jejich závěru. V tomto případě se do kolečka dopíše číslo udávající počet hodů, dokud se neobjeví jednička (včetně hodu s 1). Žáci asi řeknou: “To číslo v kroužku říká, v kolikátém hodě padla jednička”.
Úloha 3:
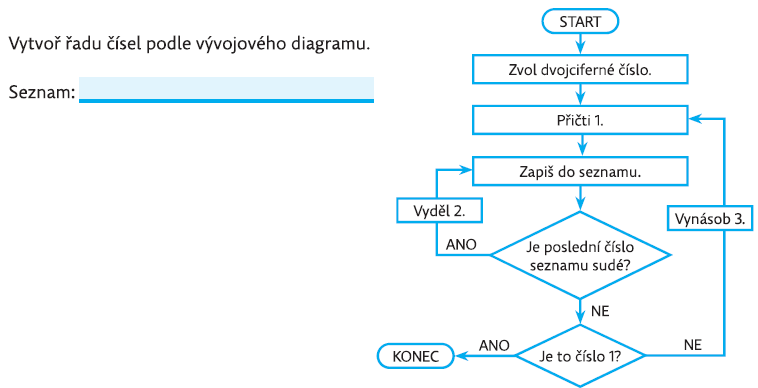
Úloha 3 je náročnější oproti úloze 2, protože obsahuje dva rozhodovací bloky. Tím se dají úlohy dobře gradovat. Zde není úplně jednoznačná interpretace vývojového diagram, spíše s žáky lze řešit délku jednotlivých procesů. Dá se např. doplnit úlohy: “Najdi dvojciferné číslo takové, aby počet čísel v seznamu byl co nejkratší. Nebo naopak co nejdelší”. Taková úloha vyžaduje spoustu experimentování i početních úloh.
Úloha 4:
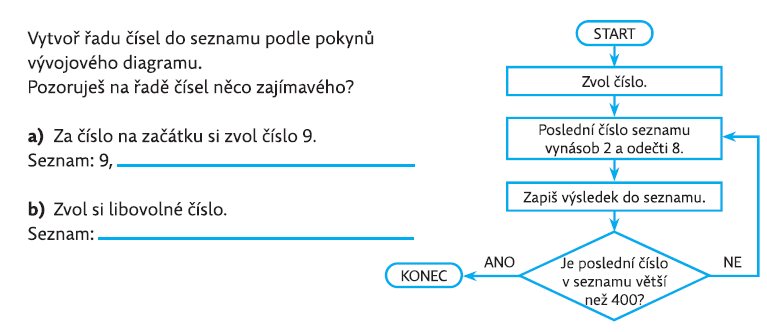
Pokud žáci vypíší postupně seznam čísel, dostanou 9, 10, 12, 16, 24, 40, 72, 136, 264, 520. Pak proces končí. Zajímavé je, že rozdíl sousedních čísel se postupně zdvojnásobuje: 9 a 10 mají rozdíl 1, 10 a 12 rozdíl 2, 12 a 16 rozdíl 4, atd.
Žáci mohou dále experimentovat. Pokud zvolí jako vstup číslo 8, proces nikdy neskončí (8, 8, 8, 8,….). Nebo pokud žáci vezmou velké číslo, seznam má pouze dvě čísla apod. Pokud žáky takové úlohy baví, je to skvělá příležitost k experimentům a mnohému počítání.
Zajímavé je, pokud si žáci vyberou číslo menší než 8. V takovém případě zjistí, že se posloupnost čísel zmenšuje. Opět si mohou všimnout, že se postupně rozdíly mezi sousedními dvěma čísly zdvojnásobují: 6, 4, 0, -8, -16,… Navíc, taková posloupnost v našem vývojovém diagramu nikdy neskončí, protože u klesající posloupnosti budou čísla stále menší a menší a nikdy nebudou větší než 400.
Úloha 5:
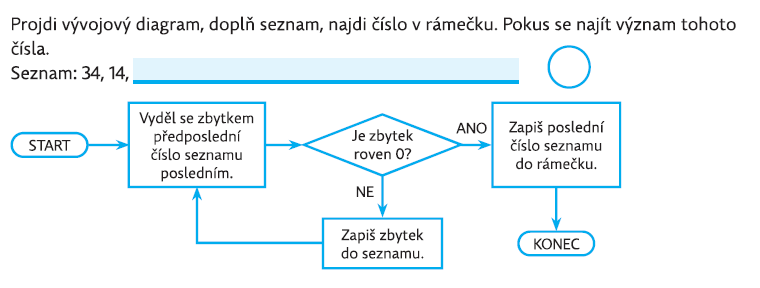
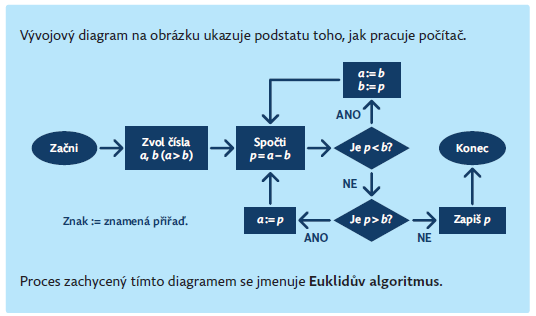
Dalším příkladem je známý vývojový diagram. Ten z hlediska matematiky popisuje, jak určit největší společný dělitel dvou čísel, zde konkrétně čísel 34 a 14. Projitím algoritmu vyjde číslo 2.
Pozn.: Tento postup hledání největšího společného dělitele dvou čísel je nazýván Euklidův algoritmus. Dá se i hezky vizualizovat. Srovnejme vývojový diagram na dalším obrázku s následnou úlohou.
Úloha 6:
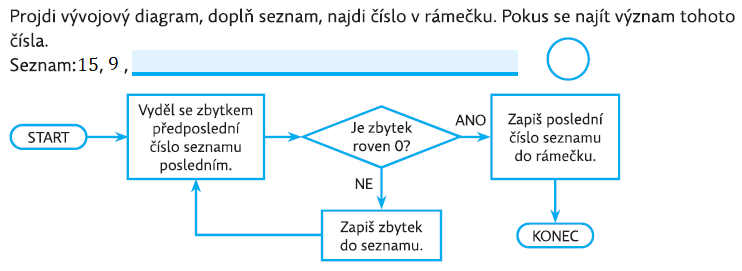
Úloha 7:
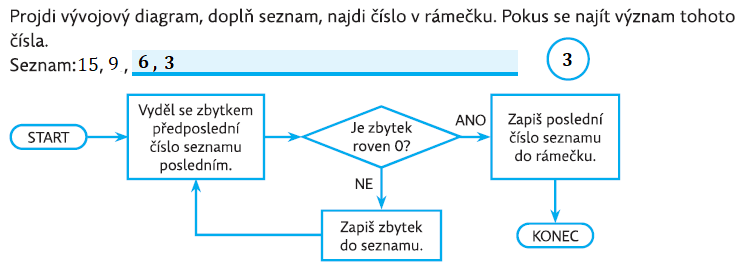
Na obrázku je obdélník 15 x 9. Postupně z něj odděluj co největší čtverce. Jaké jsou rozměry vzniklých čtverců? Jaký je nejmenší?
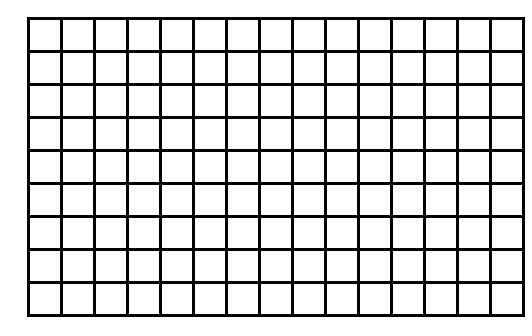
Na první pohled nemusí být jasná souvislost úloh 6 a 7. Ale obě jsou z hlediska matematiky “totožné” a slouží k odhalení největšího společného dělitele čísel 15 a 9. Když s žáky toto téma probíráme, je možné i vhodné takové souvislosti žákům nabídnout.
Úloha 6:
Úloha 7:
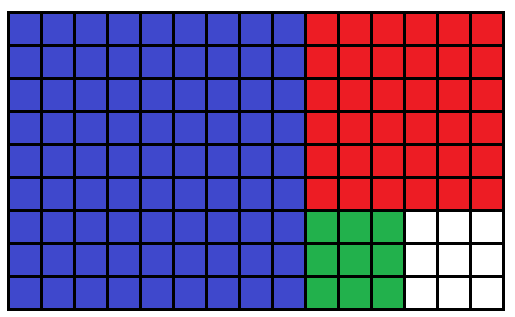
Strana nejmenšího čtverce (3) ukazuje největší společný dělitel čísel 15 a 9.
Úlohy s vývojovými diagramy lze také propojit s úlohami z prostředí Posloupnosti, které se lámou. Vezměme si úlohu přímo z blogu Posloupnosti, které se lámou, úloha 2 c).
Úloha 8:

Žáci postupně doplní:
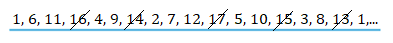
Úloha 9:
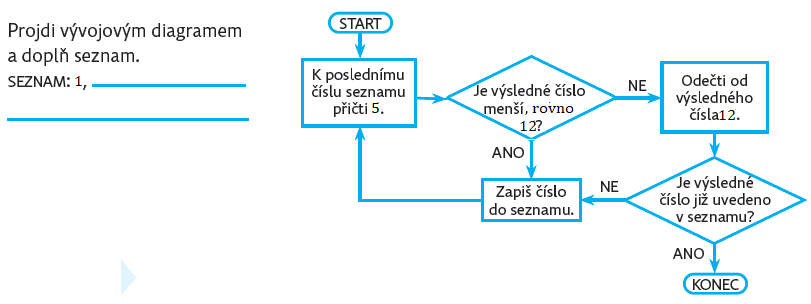
Procházením vývojového diagramu se žáci dostanou ke stejným číslům jako v úloze 8. S tím rozdílem, že ve vývojovém diagramu nejsou evidována škrtnutá čísla (tedy čísla, která jsou větší než 12).
Vývojové diagramy jsou vhodnými výzvami pro tvorbu úloh. Speciálně motivovaní žáci mohou pro spolužáky vymýšlet různé výzvy. Je ale potřeba, aby před vlastní tvorbou měli s diagram již bohatší zkušenosti.
Na druhém stupni se objevuje trochu v jiné úpravě úloha 5. Ta vede ke zmíněnému Euklidovu algoritmu. Na úloze je ale dobře vidět posun v použitém jazyce. Dovedeme si představit, že provedení této úlohy by pro žáky bylo těžko stravitelné 1. stupně.