
Prostředí:

Prostředí:
Od násobilky k algebře
Prostředí násobilkových čtverců začíná až ve 2. ročníku. Je důležité nejen pro operaci násobení, ale i pro dělitelnost a algebru.
Úloha 1: Násobilkový čtverec na obrázku má čtyři rohová čísla (v modrých polích) a čtyři středová čísla (ve žlutých polích).
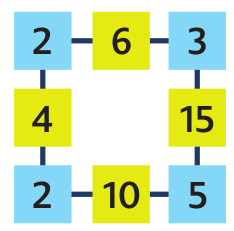
a) Vysvětli, jak ze čtyř rohových čísel můžeme najít všechna středová čísla.
b) Vysvětli, jak ze čtyř středových čísel můžeme najít všechna rohová čísla.
Úlohu a) vyřeší žáci snadno.
Trochu náročnější je úloha b), protože zde nejde o jednoduché násobení, ale o rozklad čísla na součin. Někdy hned na první pokus žák správně rozloží horní číslo 6 na 2 × 3 a zbytek již jde lehce. Někdy se to povede až na druhý pokus.
Úloha 2: Doplň scházející čísla.
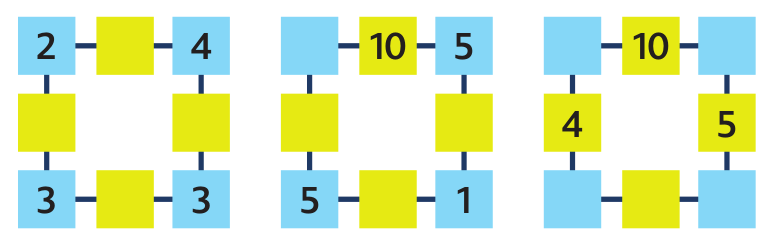
Horní řádek náročnější úlohy c) je stejný jako u čtverce z úlohy b). To napoví řešení. Všechny úlohy, které jsme zatím řešili, měly vždy jediné řešení. Následující úloha jich bude mít více.
Úloha 3: Vytvoř si násobilkový čtverec. Všechna čtyři středová čísla jsou stejná: 6. Najdi všechna rohová čísla.
Když horní levé rohové číslo žák zvolí 1 (2, 3, nebo 6), lehce dopočítá zbylá tři rohová čísla. Na papíře teď leží čtyři řešení a žák se ptá, zda ta dvě, ve kterých máme dvě jedničky a dvě šestky, jsou různá, nebo stejná. Odpovíme, že je na něm, jak si to zvolí. Když se rozhodne považovat je za stejná, protože jedno je jen pootočením druhého, bude úloha mít jen 2 řešení. V opačném případě bude mít řešení 4.
Úloha 1:
a) jde o násobení
b) jde o rozklad čísla na součin.
Úloha 2:
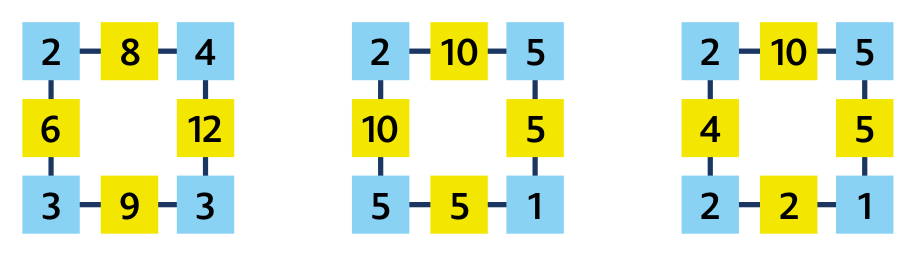
Úloha 3: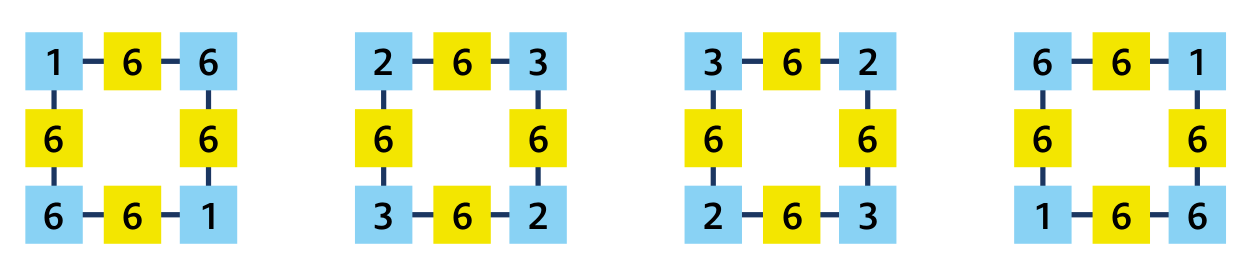
Úloha 4: V násobilkovém čtverci je horní středové číslo 18. Další dvě středová čísla jsou 27 a 81. Najdi čtvrté středové číslo a doplň rohová čísla. Hledej více řešení.
Náročná úloha. Žák nejprve zjistí, že dolní středové číslo musí být buď 27, nebo 81. Když je dolní středové číslo 27 a pravé středové je 81, tak levé středové vychází 6. Teď má úloha 2 řešení.
Když je dolní středové číslo 81 a pravé středové je 27, tak levé středové vychází 54. Teď má úloha 3 řešení.
Úloha 5: Doplň číslo v červeném rohu tak, aby součet všech čtyř středových čísel byl a) 9, b) 12, c) 15, d) 21, e) 30, f) 54.
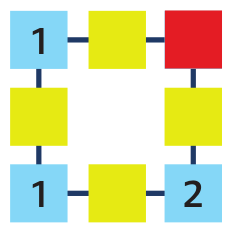
Začínáme pomocí série úloh odhalovat hlubší zákonitosti tohoto prostředí. Do pravého horního rohu žák postupně dosadí čísla 1, 2, 3… a odhalí vztah mezi dosazeným číslem a součtem čtyř středových čísel.
Úloha 6: Ve čtverci z úlohy 5 změň horní číslo 1 na 2. Když do červeného pole doplníš 1 a najdeš čísla středová, bude jejich součet 8. To je v prvním sloupci tabulky. Doplň tabulku:

Úloha 7: Ve čtverci z úlohy 5 změň číslo 2 na 3. Pro tento čtverec vytvoř stejnou tabulku jako v úloze 6. Obě tabulky porovnej.
To, že jsou obě tabulky stejné, musí mít nějakou příčinu. Potřeba žáka odhalit toto tajemství je hlavním cílem úlohy 7. Nápovědou k hledání tajemství je následující úloha.
Úloha 8: Čtverce zkoumané v úlohách 6 a 7 vedou ke stejné tabulce. Najdi ještě jiný čtverec (v dolním levém poli je 1, do horního levého a dolního pravého čtverce dáš vhodná čísla), který povede ke stejné tabulce.
Úloha 4:

Úloha 5:
a) 2, b) 3, c) 4, d) 6, e) 9, f) 17 – číslo v červeném poli = součet středových čísel : 3 – 1.
Úloha 6: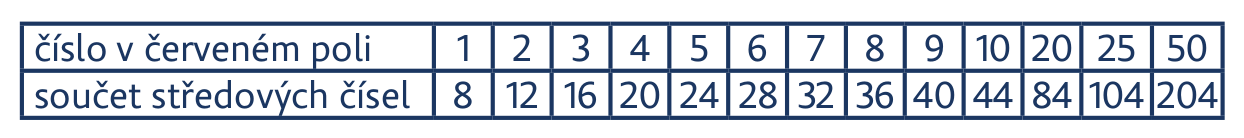
Úloha 7:
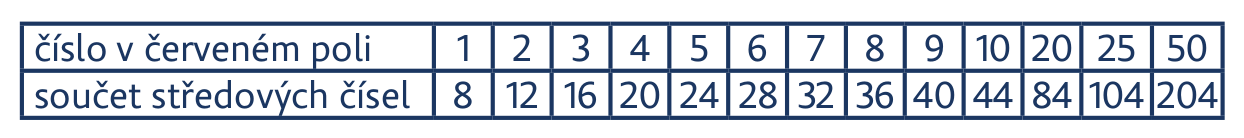
Úloha 8:
Musí platit, že (b + d) = 4, a to je možné 5 způsoby:
a) b = 0, d = 4; b) b = 1, d = 3; c) b = 2, d = 2 (Úloha 6); d) b = 3, d = 1 (Úloha 7); e) b = 4, d = 0.
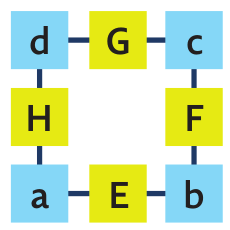
Čísla v násobilkovém čtverci označíme písmeny tak, jak vidíme na obrázku. Hledáme dva klíčové vztahy:
1) jak ze znalosti čísel E, F, G najít číslo H.
2) jak ze znalosti čísel a, b, c, d rychle najít číslo E + F + G + H.
Vím o žákovi druhého ročníku, který přinesl do třídy klíčový vztah 2). Získal jej od rodiče. V domnění, že dělá synovi dobře, ublížil mu. Podobně, jako kdyby za něj snědl čokoládu. Ochudil dítě o radost z objevu, nebo z podílení se na společném objevu se spolužáky.
Úloha 9: Najdi H a F, když znáš E = 1 a a) G = 4; b) G = 20. Hledej všechna řešení.
Úloha 10: Najdi H a F, když znáš a) E = 4, G = 5; b) E = 16, G = 27.
Hledej všechna řešení.
Žáci, kteří vyřešili poslední úlohu 10b), již asi odhalili klíčový vztah 1).
Úloha 11: Najdi vztah, kterým jsou vázána středová čísla E, F, G, H. Vztah dokaž. Poslední úloha ukazuje cestu k odhalení klíčového vztahu 2).
Úloha 12: Najdi přirozená čísla tak, aby součet E + F + G + H byl a) 10, b) 14, c) 22, d) 26, e) 12, f) 60, g) 120.
Hledej více řešení.
Úloha 9:
a)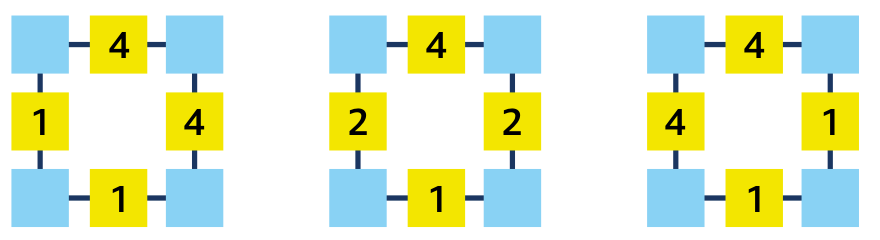
b)
Úloha 10:
a)
b)
Úloha 11:
E · G = H · F tedy H = E · G : F
Úloha 12:
Pro kontrolu uvádíme počet řešení jednotlivých úloh: a) 3 řešení; b) 4 řešení; c) 5 řešení; d) 6 řešení; e) 5 řešení; f) 66 řešení; g) 192 řešení.
E = a · b; F = b · c; G = c · d; H = d · a tedy E + F + G + H = a · b + b · c + c · d + d · a což je po úpravách (a + b) · (b + d). Jinak řečeno, když sečteme rohové číslo a s číslem c a rohové číslo b s číslem d a tyto součty vynásobíme, dostaneme součet středových čísel E + F + G + H.