Číselná osa

První setkání s číselnou osou žák prožívá v prostředí Schodů. 

Žáci řeší mnoho úloh pohybem na číselné ose, ale říkají tomu krokování na schodech, neboli na krokovacím pásu s čísly. Těmto zkušenostem předcházejí mnohé zkušenosti získané z řešení úloh v Krokování, a tedy na krokovacím pásu bez čísel.

Úloha 1:

První setkání s číselnou osou žák prožívá v prostředí Schodů. Na obrázku jsou sice znázorněné schody a po realizaci úloh na skutečných schodech si je žáci vymodelují ve třídě jako krokovací pás s čísly.

Žáci řeší mnoho úloh pohybem na číselné ose, ale říkají tomu krokování na schodech, neboli na krokovacím pásu s čísly. Těmto zkušenostem předcházejí mnohé zkušenosti získané z řešení úloh v Krokování, a tedy na krokovacím pásu bez čísel.

Úloha 2:

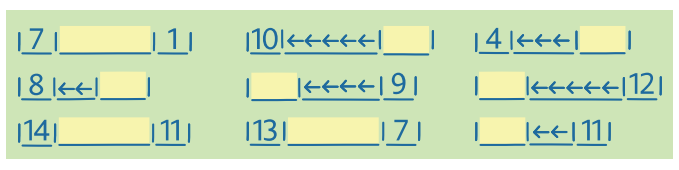
V prostředí Schody se řeší i úlohy náročnější, které dávají dětem dobré zkušenosti, které využijí při práci s číselnou osou. V 1. ročníku upřednostňujeme tuto variantu (sémantizované) číselné osy, to znamená, že čísla vyjadřují “název” / ”adresu” schodu. Navíc žáci získávají zkušenosti prožitkem, tj. pohybem vlastního těla.

S obvyklou podobou číselné osy, kde čísla jsou již abstraktní, se žáci setkají až ve 2. ročníku.

Úloha 3:

V těchto úlohách žáci doplní číselnou řadu a zvědomují si její lineární uspořádání a stejnou vzdálenost mezi sousedními čísly. Čísla jsou zde v abstraktní podobě, ale když některý žák poukáže na to, že je to stejné jako u Schodů, učitel tuto myšlenku podpoří. Je to důležité pro vytvoření sémantické představy o abstraktním pojmu, což je předpoklad dobrého porozumění.

Úloha 4:

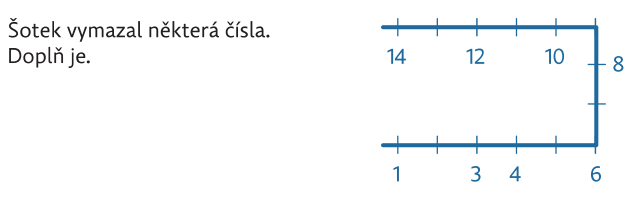
Touto úlohou se bourá předsudek, že číselná osa musí jít pouze zleva doprava.

I ve 2. ročníku žáci vedle těchto úloh řeší velké množství úloh v prostředí Krokování a Schodů.

Úloha 5:

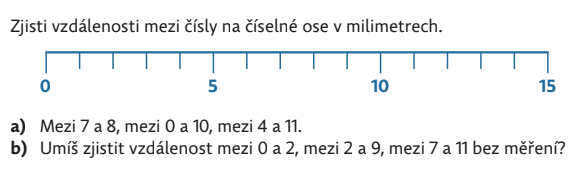
Číselná osa je využita i pro měření v milimetrech. Aby žáci zjistili vzdálenosti mezi čísly, je potřeba alespoň jednou měřit.

Žáci mohou vyznačit všechna čísla na číselné ose a změřit požadované vzdálenosti. Přínosnější však je změřit vzdálenost dvou sousedních čísel (1 dílek) a pak vhodným číslem násobit. Tím žáci získávají zkušenosti s přímou úměrností. Ze znalosti délky jednoho dílku počítají délku např. sedmi dílků.

Úloha 6:

Dále je číselná osa využita pro otevření myšlenky zaokrouhlování. Rozdíl dvou čísel je vizualizován vzdáleností dvou bodů. Silně vyznačená jsou ta čísla, vzhledem ke kterým se budou čísla zaokrouhlovat. Např. číslo 12 je blíže k číslu 10 než 20, tedy 12 se bude zaokrouhlovat na 10.

Úloha 7:

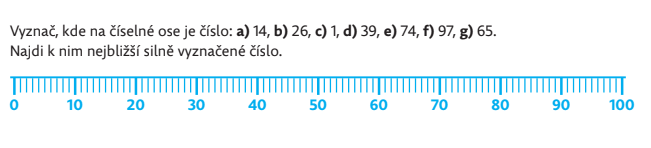
Pokračujeme v otevírání myšlenky zaokrouhlování čísel. Jako vhodná pomůcka pro tuto činnost slouží metr (např. papírový, skládací, svinovací). 

Ve všech úlohách kromě poslední je výsledek jednoznačný. U čísla 65 nastane pravděpodobně diskuze. Tato úloha má dvě možná řešení – číslo 60 i 70. Z matematického hlediska jsou obě řešení stejná, žádné nelze upřednostnit. Zatím necháme ve hře obě možnosti, ale trochu později zavedeme dohodu, která tyto dvě možnosti ošetří. Tato dohoda zní: Číslo, které končí na 5, se zaokrouhluje nahoru. Např. číslo 135 se na desítky zaokrouhlí na 140.

Úloha 8:

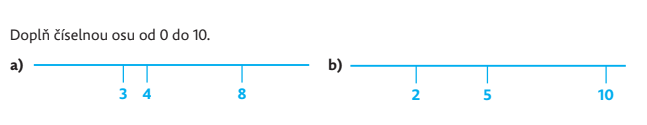
Žák může použít měření nebo si na papírek vyznačí vzdálenost dvou čísel, nejlépe sousedních čísel. Tuto vzdálenost pak přenáší. U úlohy b) má žák více možností, proto je užitečné hledat více způsobů řešení. Např. může využít vzdálenosti mezi 5 a 10, z toho najde 0, z 0 a 2 najde 4 a má dvě po sobě jdoucí čísla 4 a 5. Nebo využije vzdálenosti mezi 2 a 5, z toho najde 8 a pak od 10 najde 7 a už má po sobě jdoucí čísla 7 a 8.

Úloha 9:

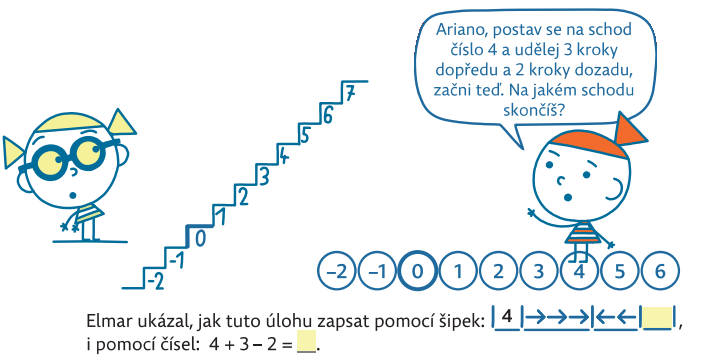
Při otevírání kognitivně náročnější látky, což jsou záporná čísla, se vracíme do sémantiky, tj. do krokování na schodech. Tímto způsobem se rozšiřuje i číselná osa o záporná čísla, jak je vidět v následující úloze.

Úloha 10:

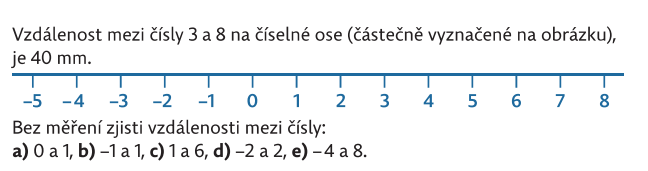
Porozumění práci na číselné ose podporuje průběžné řešení velkého množství úloh v prostředí Krokování a Schodů.

Číselná osa je významnou pomůckou pro řešení úloh o věku. Např. Aničce jsou 3 roky. Až jí bude tolik, kolik je Honzíkovi, Honzíkovi bude 11 let. Kolik je dnes Honzíkovi.

Úloha 11:

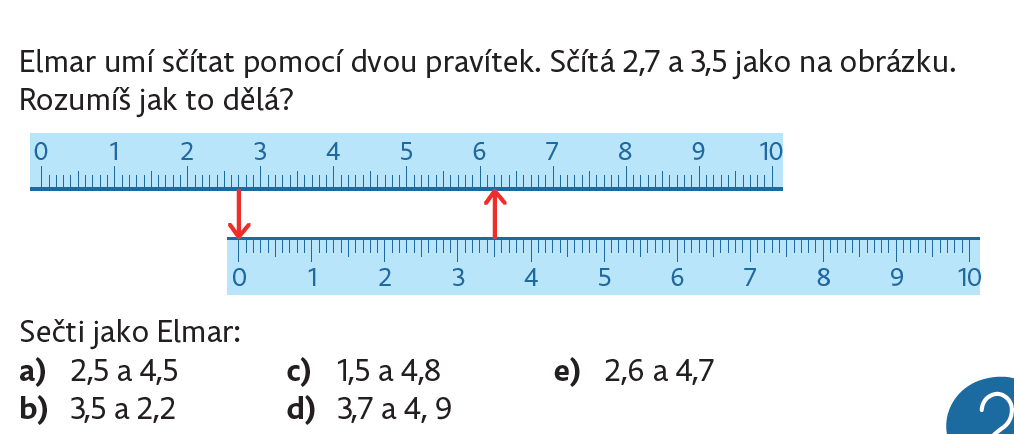
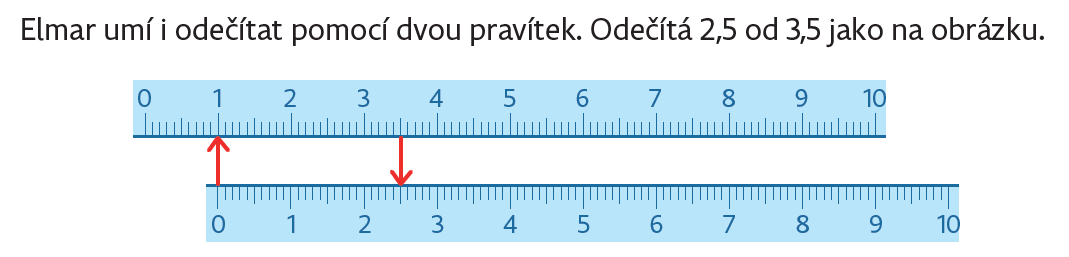
Číselnou osu, která může být reprezentovaná i měřítkem, lze využít pro sčítání a odčítání dvou čísel, i desetinných. Sčítání/odčítání je modelováno jako grafický součet/rozdíl dvou úseček.

Práce na číselné ose spolu s krokováním pomáhá s porozuměním uchopit úlohy v prostředí Mříže, např. při vyvození souřadnic mřížových bodů a práci s nimi.