Prostředí:
Egyptské dělení
V prostředí se žáci aktivně i pasivně setkají s množstvím důležitých myšlenek týkajících se zlomků.
Prostředí:
Zlomky se objevovaly již v dávné minulosti. Ve starověkém Egyptě se tisíc let pracovalo pouze se zlomky kmenovými, tzn. zlomky ve tvaru 1/n, kde n je přirozené číslo. Takže Egypťané znali polovinu, třetinu, čtvrtinu, ale např. ¾ neznali. Ty získali díky kmenovým zlomkům, např. ¾ = ½ + ¼.
Jako v historii, poznávání zlomků žáky by mělo probíhat stejně. Proto se při prvních zkušenostech se zlomky klade důraz na tyto kmenové zlomky. Dobrým průvodcem (nejen kmenovými zlomky) je prostředí Egyptské dělení chleba.
V prostředí se žáci aktivně i pasivně setkají s množstvím důležitých myšlenek týkajících se zlomků. Při řešení úloh se objeví sčítání i odčítání zlomků, konstrukce typu 2/3 = 2 · 1/3, rozšiřování a krácení zlomků nebo se také připravuje násobení zlomků (např. co je to třetina z poloviny).
Když ve 4. ročníku zavádíme prostředí Egyptské dělení chlebů, požadujeme, aby:
Později, v 5. ročníku, přibude ještě podmínka: 3. nikdo nesmí dostat dva stejné kusy chleba.
Úloha 1:
Rozděl dva chleby mezi tři podílníky. Zapiš pomocí zlomků, jaké části mohl dostat jeden
podílník.
Úlohu lze uvést motivačním příběhem: ”Tři chudí Egypťané Kiress, Elmarir a Arianos společně pracovali celý den na poli. Po práci si mohli dohromady dovolit koupit jen dva egyptské chleby (kulaté placky). O ty se spravedlivě podělili. Navrhněte, jak to mohli udělat.”
Úloha 2:
Jak vypadá řešení předchozí úlohy, u kterého jsou k rozdělení potřeba právě 4 řezy?
Úloha 1:
Řešení je více, ale předpokládáme, že se objeví zejména tyto tři:
Diskutujeme, zda jsou všechna řešení správně, čím se liší, případně které se žákům jeví být nejlepší a proč. První dvě uvedená řešení odpovídají podmínkám 1) a 2). Žáci řešení doplní o matematický zápis. Tedy u prvního rozdělení chlebů dopíšou, že každý z podílníků dostane 1/3 + 1/3 chleba. U druhého rozdělení dopíšou ½ + 1/6 chleba. Poslední z uvedených řešení nesplňuje podmínku 2). Dva podílníci dostanou svůj díl v jednom kuse a třetí ve dvou kusech. Seznámení se s prostředím výrazně urychlí manipulativní činnost žáků. Mohou dělení chlebů modelovat stříháním papírových kruhů, používat dřevěné či pěnové kruhové zlomky nebo si mohou situaci kreslit.
Úloha 2:
Úloha se vrací k předchozí úloze. Cílem je vyvolat diskuzi o počtu řezů. V prvním řešení je 6 řezů a ve druhém jsou pouze 4. Zde je nutná domluva, jak evidovat počet řezů, která nemusí odpovídat životní zkušenosti žáků. Například zde na obrázku je vidět, jak chléb rozdělíme na čtvrtiny pomocí tří řezů.
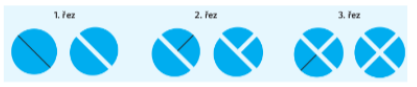
Vraťme se k výše zmíněným řešením:
Obě řešení se liší také tím, že v prvním případě dostane každý podílník dva stejné kusy (1/3 + 1/3). Ve druhém případě dostane dva různé kusy (½ + 1/6). Učitel sdělí, že ve starém Egyptě usilovali o co nejmenší počet řezů a měli podmínku, že nikdo nesmí dostat dva stejné kusy chleba → tím zkompletujeme výše uvedené podmínky. Po žácích zatím nevyžadujeme dodržování poslední podmínky, čímž získáme více různých řešení. Žáci tak obohacují své zkušenosti se zlomky.
V pátém ročníku se vracíme k zavedení prostředí.
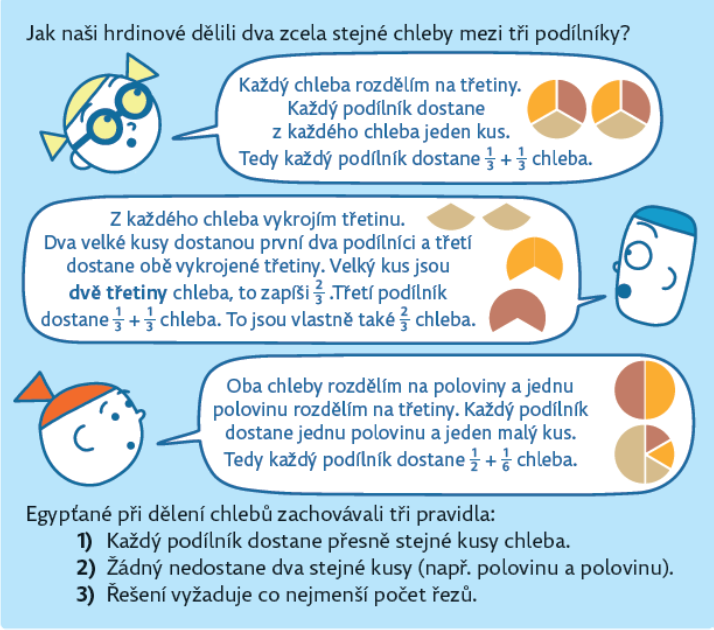
První úloha je spíše diskuzní mezi žáky. Žáci komunikují o tom, která z řešení našich postaviček odpovídají třem egyptským pravidlům.
Úloha 3:
Která z pravidel zachovává řešení a) Ariany, b) Elmara, c) Kiry?
V další úloze se žáci dostávají již do role Egypťanů a realizují dělení chleba. Objevují se různá řešení, např. v úloze a) ¾ = ¼ + ¼ + ¼ nebo ¾ = ½ + ¼. Žáci se domluví, které řešení je z pohledu pravidel “lepší”. Je ale žádoucí nechat žákům volný prostor k řešení a pravidly je v začátcích neomezovat. Např. řešení ¾ = ¼ + ¼ + 1/4 ukazuje žákům důležitou konstrukci ¾ = 3 · ¼. Pokud bychom taková řešení zakázali pravidlem, žáci by se k takovým zkušenostem nedostali.
Žáci také prvními zkušenostmi s úlohami přijdou na to, že část, kterou dostane každý podílník lze poznat přímo ze zadání: např. v úloze b) 4/6, v úloze c) 5/8 atd.
Úloha 4:
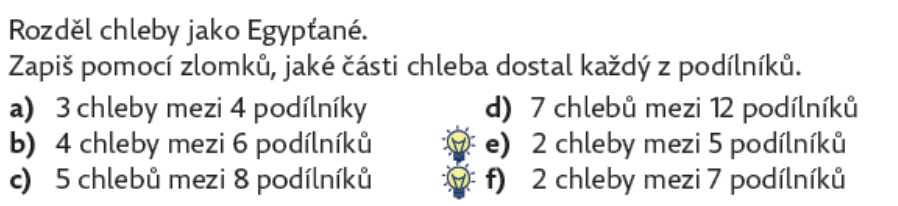
Úlohy s dělením chlebů se objevují i na druhém stupni.
Úloha 4:
a) ½ + ¼,
b) ½ + 1/6,
c) ½ + 1/8,
d) ½ + 1/12,
e) 1/3 + 1/15,
f) ¼ + 1/28
Úloha 5:
Žáci řešením úlohy objeví jistou pravidelnost. Zadání úloh se totiž mění pravidelně (chleby narůstají po jednom, podílníci po dvou). To umožňuje i zobecnění řešení: “Každý podílník dostane polovinu chleba a pak ještě 1/(dvojnásobek počtu podílníků)”.
Podobně lze vytvářet podobné série úloh, které vedou k nalezení určitého pravidla.
Úloha 6:
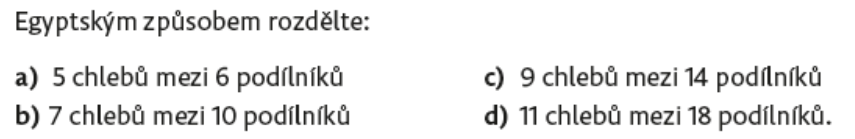
V některých sériích může být objevení takové pravidelnosti náročnější.
Úloha 7:
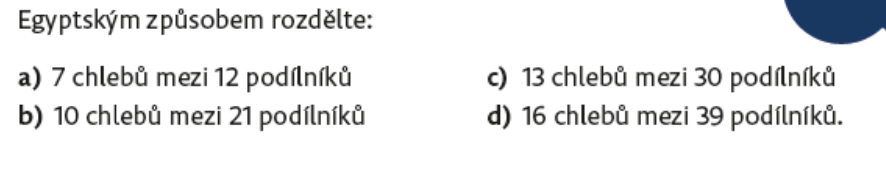
Úloha 5:
a) ½ + 1/14,
b) ½ + 1/18,
c) ½ + 1/22,
d) ½ + 1/26
Úloha 6:
a) ½ + 1/3,
b) ½ + 1/5,
c) ½ + 1/7,
d) ½ + 1/9
Úloha 7:
a) ½ + 1/12,
b) 1/3 + 1/7,
c) 1/3 + 1/10,
d) 1/3 + 1/13. Zobecnění se objeví až s řešením úlohy a) 1/3 + ¼.