Kameny

V Evropě se ještě v 16. století pracovalo s římskými čísly než Arabové přinesli indický způsob zápisu čísel, který se ukázal být výrazně efektivnější ze dvou důvodů:

1. pomocí něj bylo možné zapsat libovolně velké číslo s použitím deseti znaků (cifer 0, 1, 2, ..., 9);
2. základní početní operace (+, -, ·, :) se prováděli mnohem snadněji než pomocí římských čísel.

Podstata indického zápisu čísla spočívá v tom, že stejná číslice představuje různou hodnotu podle pozice v čísle. Např. číslice 2 v čísle 2 111 představuje 2 000, v čísle 1 211 představuje 200, v čísle 1 121 představuje 20 a v čísle 1 112 představuje 2. Žák ve třetím ročníku již dokáže pracovat s trojmístnými čísly, ale podstatu poziční soustavy si neuvědomuje. Úlohy z prostředí Kameny se snaží žákovi otevřít první porozumění pro poziční soustavu.

Nejprve se žáci seznámí s naší pomůckou. Čtou čísla vytvořená kameny a pomocí kamenů tvoří čísla, které řekne učitel nebo spolužák. Situace je ilustrována na obrázku u úlohy 1.

Úloha 1:

Žáci mají připravené pomůcky (např. pokladničky o třech přihrádkách, papír s danou tabulkou apod. a dále tři objekty – např. kaštany, víčka, kamínky, ... ). Pak pomocí tabulky a tří kamenů tvoří různá čísla. Žáci tak pracují s vizuální reprezentací čísla, ve které jsou zdůrazněny řády čísla. Vytvořením čísla si zvědomují hodnotu na jeho pozici v zápise. Pracují tedy se zápisem čísla v poziční desítkové soustavě. Hledáním všech řešení se dostáváme do oblasti kombinatoriky a práce s daty. Žáci pravděpodobně budou úlohu řešit náhodným sestavováním čísel, někteří i systematičtěji. Jak se ale přesvědčí, že jejich seznam řešení je úplný a žádné číslo se v něm neopakuje? Musí nějak soubor čísel organizovat. Například podle velikosti. Zajímavé je porovnat různé způsoby řešení a ptát se, kterému způsobu hledání všech možností žáci nejlépe rozumí. Je možné dát úlohy s většími počty kamenů nebo do tabulky přidat i řád tisíců. Někteří žáci zdokonalují své řešitelské strategie a volí více systematické postupy. O ty se v diskuzi podělí se třídou.

Úloha 2:

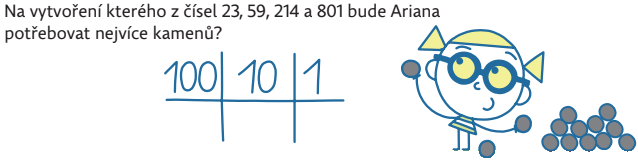
Velice pravděpodobně žáci odhalí, že počet kamenů na vymodelování čísla je určen součtem číslic daného čísla. Otevíráme tak myšlenku ciferného součtu čísel, který budeme potřebovat později pro otázky dělitelnosti.

 Zde lze vytvářet i sofistikovanější úlohy, například: Na vymodelování čísla a je třeba 7 kamenů. Na vymodelování čísla b je třeba 6 kamenů. Na vymodelování čísla a + b jsou třeba 4 kameny. Najděte čísla a, b.

Úloha 3:

Přidáváme podmínku s ciferným součtem, kterou však formulujeme přijatelnějším jazykem. I tak je úloha na první pohled složitá. Po vypsání všech dvojciferných čísel vytvořených pomocí 4 kamenů: 40, 31, 22 a 13 je řešení nasnadě. Žáci nabývají zkušenost s tím, že pokud si úlohu rozloží na dílčí kroky, získají do problému hlubší vhled. Poté přichází obdobné úlohy již s většími počty kamenů a většími rozdíly.

Úloha 4:

Dalším cílem úloh z prostředí Kameny je připravit žáky na porozumění kritériím dělitelnosti. Cílem uvedené úlohy je jednak mnohé počítání, ale také získávání zkušeností se společnými črty čísel dělitelných třemi. Žáci zjistí, že přidáním jednoho kamene se jim nepodaří vytvořit žádné číslo, které lze dělit třemi beze zbytku (mohou vytvořit čísla 311, 221, 212). Ubráním jednoho kamene mohou vytvořit čísla: 210, 201, 111 a ty lze všechna dělit třemi beze zbytku.

Později přichází úlohy Která trojciferná čísla vymodelována pomocí šesti kamenů jsou dělitelná 3? Která trojciferná čísla vymodelována pomocí devíti kamenů jsou dělitelná 3? a s nimi také další zkušenosti s čísly dělitelnými třemi. Po několika pokusech žáci zjistí, že každé rozložení např. šesti kamenů do tabulky dá číslo dělitelné 3. Třída začne hledat takové rozložení kamenů, aby číslo nebylo dělitelné třemi. Hledání je neúspěšné. V třídní diskuzi postupně zjišťují, že všechna čísla vytvořená ze šesti kamenů jsou dělitelná třemi. Zákonitost objevili, ale její zdůvodnění zatím neznají. To zjistí později, když trojciferné číslo ABC přepíší do tvaru 100A + 10B + C. To se rovná (99A + 9B) + A + B + C. První závorka je jistě dělitelná třemi. Tedy celé číslo je dělitelné třemi, když číslo A + B + C je dělitelné třemi. V našem případě A + B + C je 6 (kamenů). Učitel postupně může měnit počet kamenů, rozšiřovat tabulku o řád tisíců, statisíců apod. Žáci experimentují a když mají dost zkušeností, objeví, že čísla dělitelná třemi jsou ta složená ze 3, 6, 9 atd. kamenů. Tím vlastně objeví a pojmenují kritérium dělitelnosti číslem 3.

Úloha 5:

Pokračujeme v rozšiřování zkušeností potřebných pro vyvození kritérii dělitelnosti i jinými čísly než číslem 3. Žáci zjistí, že třemi jsou dělitelná všechna čísla a dvěma ta, kde na místě jedniček není žádný kámen, 2 kameny nebo 4 kameny.

O něco později následuje analogická úloha Která trojciferná čísla vymodelována pomocí šesti kamenů jsou dělitelná číslem 6? Pokud si některý žák všimne, že řešení u obou úloh je stejné, o své zjištění se podělí s třídou.

Úloha 6:

Úlohy se opakují v různých variacích, aby žáci měli víc možností pro získaní potřebných zkušeností k vyvození pravidel dělitelnosti, nebo aby mohli již objevené pravidlo aplikovat.

Úloha 7:

Cílem úlohy je nabití zkušeností potřebných pro vyvození kritérii dělitelnosti číslem 9.