
Prostředí:

Prostředí:
Jak prohloubit porozumění složitým vztahům
Prostředí Rodina se věnuje jak prohlubování porozumění vztahům, tak početním dovednostem. K tomuto prohlubování dochází při individuální činnosti i během diskuzí. Je důležité respektovat názory dětí, ponechat jim autonomii, podpořit je vlídným slovem a nechat je obhájit si své přesvědčení.
Pro dvouleté dítě slovo máma označuje jednu konkrétní osobu. Pětileté dítě ví, že i kamarád má mámu, ale je překvapeno, že babička je mámina máma. Dítě, které chápe slovo máma jako vztah dvou osob, rozumí tomuto slovu již na úrovni abstrakce. Podobně rozumí slovům otec, dcera, syn, sestra… Těmto dětem můžeme dávat úlohy z jejich rodiny:
Úloha 1: Kdo je syn/dcera tvé mámy?
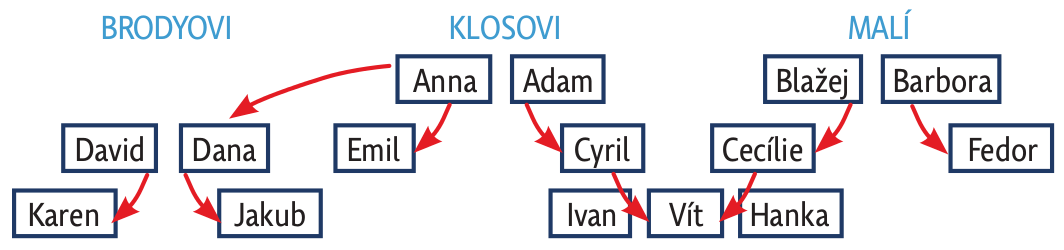
Abychom byli schopni všechny základní rodinné vztahy prozkoumat, musíme vycházet z „umělé rodiny“, ve které tyto vztahy jsou. Výše je zobrazen rodokmen. Předškolákovi z něj vybereme pouze Cecílii, Cyrila a jejich tři děti. Když dítě tento rodokmen pochopí, může dostat úlohu:
Úloha 2: Někdo řekl: „Vítek je můj syn.“ Kdo to řekl?
Dítě, které odpoví, že Cecílie (nebo Cyril), odpovědělo dobře. Vyspělejší dítě uvede oba rodiče.
Do rodokmene přibydou všichni čtyři prarodiče Anna, Adam, Blažej, Barbora a Cyrilovi sourozenci Emil a Dana.
Univerzální způsob tvorby úloh dává návod: Napište pravdivý vztah a jeden jeho objekt zakryjte. Tak ze vztahu 5 – 2 = 3 dostávám tři úlohy: 5 – 2 = ?; 5 – ? = 3; ? – 2 = 3.
Podobně z výpovědi „Hančin otec je Cyril“ vytvoříme tři úlohy:
Úloha 3: Doplň.
a) Hančin otec je ________ .
b) Hančin ______ je Cyril.
c) _______ otec je Cyril.
Úloha a) je nejlehčí. Doplní se poslední slovo „Cyril“. U složitější úlohy b) se doplňuje prostřední slovo „otec“. Úloha c) je nejsložitější, schází první slovo, které může být „Hančin“ nebo „Vítův“ nebo „Ivanův“.
Ve třetím ročníku se dozvíme o rodině Brodyových a o bratrovi Cecílie Fedorovi. Hodně otázek se zabývá věkem postav našeho rodokmenu. Ty zde oželíme.
Úloha 4: Kdo řekl: „Jsem vnučkou mámy mé mámy?“
Děti najdou odpověď Karen nebo Hanka. Najde se ovšem dítě, které řekne, že to může být i Dana nebo Cecílie nebo dokonce i Anna či Barbora, protože uvedený výrok může říct kterákoliv žena. Toto zjištění ukazuje, že u některých výroků je nutno doložit informaci, zda je chápeme pouze uvnitř našeho rodokmenu nebo obecně.
Úloha 5: Kdo řekl: „Jsem dědečkem syna svého syna.“?
Když mluvíme jen v rámci našeho rodokmenu, řešením je pouze Adam. Obecně může být řešeními Blažej, jestliže bude mít Fedor syna. Může to býti Cyril, když alespoň jeden z jeho synů bude mít syna. Zde naše úvahy vstupují do oblasti hypotéz, které přesně formulujeme takto: Bude-li mít Fedor syna, pak řešením úlohy 5. je i Blažej.
V prostředí Rodina je možné hlouběji proniknout do struktury logiky. V následující úloze jsou použity logické spojky a a nebo.
Úloha 6: Mluví Cecílie pravdu, když řekne:
a) „Fedor a Emil jsou mí švagři.“,
b) „Fedor nebo Emil je můj švagr.“ ?
O výpovědi a) žáci většinou řeknou, že je pravdivá jen částečně, protože Fedor není Cecíliin švagr, ale bratr. Přesný matematický jazyk ale výrok skládající se ze dvou částí spojených spojkou a považuje za pravdivý tehdy a jen tehdy, když oba výroky jsou pravdivé. Tudíž Cecíliina výpověď a) je výrok nepravdivý.
O výpovědi b) obvykle žáci řeknou, že je to popletené, protože Fedora sem není nutné tahat. Přesný matematický jazyk výrok skládající se ze dvou částí spojených spojkou nebo považuje za pravdivý tehdy a jen tehdy, když alespoň jeden z dílčích výroků je pravdivý. Tudíž Cecíliina výpověď b) je výrok pravdivý.
Podobně lze najít mnoho úloh, které uvádí žáky do dalších jevů logiky, jako jsou zápor (není pravda, že…), implikace (jestliže…, pak…), ekvivalence (...tehdy a jen tehdy, když…), kvantifikátory (pro všechny platí…, resp. existuje… takže platí…).