
Prostředí:

Prostředí:
Prostředí Schody obsahuje podobné myšlenky jako prostředí Krokování. Mezi oběma prostředími jsou však důležité rozdíly. V Krokování se používá krokovací pás bez čísel, v prostředí Schody pás s čísly. Číslo se zde již tedy neobjevuje pouze jako operátor (počet kroků dopředu, nebo dozadu), ale i jako adresa (číslo schodu). Tím se připravuje velice důležitý pojem – číselná osa.
Prostředí je v učebnicích zavedeno následující úlohou.
Úloha 1:
Ideální je, když se úloha realizuje na skutečných schodech. Po několika sehrávkách úloh se učitel s žáky domluví, že si přenesou čísla schodů do třídy a vytvoří tak krokovací pás s čísly. Liší se i povelová technika. První pokyn je: „Postav se na schod číslo x“. Další pokyn je stejný: „Udělej y kroků dopředu nebo dozadu“. Otázka se opět liší od krokování: Na jakém čísle schodu jsi skončil? Žáci tedy řeší úlohy na aditivní operace – sčítání a odčítání.
Po řešení několika úloh přichází potřeba úlohy a jejich řešení zapsat. Volíme opět jazyk šipek a číslem v boxu označíme číslo schodu. To, co je odlišné od Krokování, je pojmenování pohybů. Zatímco v Krokování jde o pohyb dopředu či dozadu, ve Schodech žáci díky životní zkušenosti většinou při dramatizaci na schodech použijí pohyb nahoru a dolů. Později na krokovacím pásu s čísly se žáci často vrací k používanému: krok dopředu a krok dozadu.
Úloha 2:
Úloha 3:
Na tomto obrázku se objevují různě náročné úlohy. Dospělý si může ověřit, jaká z úloh je pro dítě nejobtížnější. Pravděpodobně to budou úlohy, kde chybí počáteční číslo schodu jako je např. v úloze |___|→→→→|9|.
Některým žákům dělají tyto úlohy potíže, protože úloha nepřipouští přirozené čtení zleva doprava, ale vyžaduje čtení z druhé strany. Postaví se na schod číslo 9, udělají 4 kroky nahoru a dochází k výsledku 13. Není to problém matematický, ale problém konvence, jazyku. Reedukace je možná trojí:
1. Přečteme: Někde stojím, jdu 4 kroky dopředu a jsem na schodu číslo 9.
2. vyřešenou úlohu čte žák zleva doprava, objeví chybu.
3. simplifikace (zjednodušení) situace, např. |___|→|2|. Po vyřešení úlohy se vracíme k původní úloze.
O něco později se objeví i kroky dolů (dozadu).
Úloha 4:
Protože se zde žáci seznamují, jak pracovat s číslem jako adresou, budou připraveni na porozumění dalších úloh, kde se vyskytuje číslo jako adresa. To jsou např. úlohy, kde se počítá s podlažími paneláku, dny v měsíci apod. Připravuje se zde důležitá myšlenka – číselná osa.
Úloha 5:
Stejně jako v Krokování žáci začnou přecházet z jazyku šipek do jazyku čísel. Ten obě prostředí propojuje.
Úloha 6:
Na první úloze si můžeme ukázat rozdíl v přepisu v obou prostředích: Ve Schodech - viz obr., v Krokování by přepis z čísel do šipek vypadal takto: 4 + 6 = 10 (|→→→→|→→→→→→|=|→→→→→→→→→→|).
Úloha 1:
Ariana je na 8. schodu, Elmar na 1. schodu, Kira na 3. schodu. Kira je 5 schodů pod Arianou.
Úloha 2:
6; 4; 12; 11
Úloha 3:
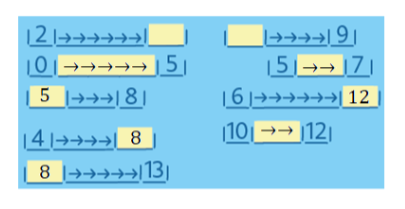
Úloha 4:
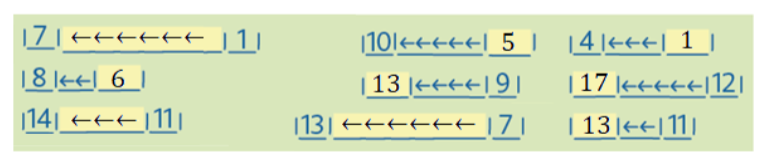
Úloha 5:
Maruška bydlí v 11. podlaží.
Úloha 6:

Úlohy lze propojit i s dalšími oblastmi matematiky. V další úloze např. úlohou, kterou lze zformulovat takto: „Stojíš na schodu 0, hoď dvakrát kostkou. Na kterém schodu skončíš? Eviduj více pokusů.“ Cílíme na práce s daty, konkrétně na sběr dat. Dovednost vytvořit si uspořádaný soubor dat se využije později ve statistice, kombinatorice a pravděpodobnosti.
Úloha 7:
Pokud žáci ve třídě nasbírají dostatečný počet pokusů (třeba přes 100), začnou se projevovat zákonitosti pravděpodobnosti. Nejvíce čárek budou mít čísla ze středu tabulky.
Později přichází i úlohy s podmínkou. Tím získávají úlohy i kombinatorický charakter (kolika způsoby lze šipky doplnit). Žáci navíc získávají zkušenost s paritou čísel (sudost, lichost). Tomu může dospělý přispět provokativní otázkou: „Vyřeš úlohu tak, abys použil šipek pět.“
Úloha 8:
Obtížnost úloh se dá zvyšovat i větším počtem povelů. Žáci jsou nuceni hledat strategie řešení, aby si úlohu usnadnili. Jednou ze strategií je strategie od konce.
Úloha 9:
Např. ve druhé úloze si všimnou, že kroků dopředu je celkem 6, kroků dozadu 3, proto úlohu mohou zjednodušit: |___|→→→|17|.
Úloha 8:
Úloha 9:
13; 14; 9; 0; -1
Po zavedení otočky čelem vzad v prostředí Krokování se otočka objeví i v prostředí Schody. Otočka a její přepis do jazyku aritmetiky je jedním z hlavních cílů obou prostředí – viz Výsledky této úlohy.
Úloha 10:
Úlohy se mohou ztížit pomocí zavedení dvojkroků. Např. na schodiště umístíme tatínka a syna. Tatínek jedním krokem překoná schody dva, syn jediný schod, jak bylo doposud obvyklé. Tatínkův „dvojkrok“ lze graficky ztvárnit např. takto: ⇒
Úloha 11:
Doplň do prázdných polí tři šipky (a výsledný schod) tak, aby stál tatínek na stejném schodu jako syn.
S: |0|______|__|
T: |3|______|__|
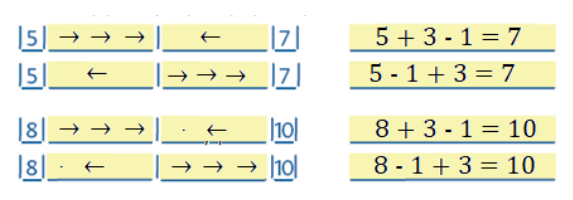
Úloha 10:
Skončí na schodu číslo 5.
Komentář: V prostředí Krokování i Schody žáci řešením úloh objeví, že otočka v přepisu do čísel odpovídá zápisu –(). Úloha se tedy přepíše takto: 2 – (1 – 3) + 1 = 5. Druhá otočka značí uzavření závorky. Pokud s žáky řešíme úlohy na skutečných schodech, úlohy s otočkou vynecháme kvůli couvání a nebezpečí možného úrazu. Vhodnější je tyto úlohy řešit na číslovaném krokovacím páse.
Úloha 11:
S: |0|→→→|3|
T: |3|___|3|
nebo
S: |0|←|-1|
T: |3| <= <= |-1|.
Na druhém stupni cílí úlohy mimo jiné i na paritu čísel (sudost, lichost). Myšlenka se objevuje v úlohách, které se ptají na počet šipek – viz následující úloha.
Úloha 12:
V prostředí Schody se objevují i úlohy, které vedou k náročnějším myšlenkám přesahující učivo základní školy.
Úloha 13:
Mirek stojí na schodu číslo 2, Terezka na schodu číslo 3. Použij právě 3 šipky tak, aby stáli na stejném schodu. Najděte všechny možnosti.
│2│________│= │3│________│
Žáci v podobných úlohách často využívají krokovací pás s čísly, úlohu si sehrají a najdou všechna řešení. Danou úlohu lze matematickým jazykem přepsat jako soustavu dvou lineárních rovnic o dvou neznámých, z nichž jedna z nich je s absolutní hodnotou: 2 + x = 3 + y, |x|+|y|=3. Je velký rozdíl mezi oběma zadáními úlohy. Úlohy s absolutní hodnotou jsou často pro žáky obtížné, řešení pomocí krokovacího pásu umožní úspěch více žákům.
Úloha 12:
Žáci zjišťují, že pokud jsou dvě čísla sousední, např. 3 a 4, je nutno použít lichý počet šipek. Pokud jsou sudý počet kroků od sebe, je nutno použít sudý počet šipek.
Úloha 13:
a) Mirek udělá dva kroky dopředu, Terka jeden dopředu;
b) Mirek udělá jeden krok dozadu, Terka dva dozadu.
Pomocí rovnic zapíšeme vztahy x = 1 + y a |x|+|y|=3. Po odstranění absolutních hodnot bychom řešili soustavu, kde jedna z rovnic je x = 1 + y, a druhá je jedna z rovnic: x + y =3, x – y = 3, -x + y = 3, -x – y = 3. Vyjdou dvě řešení x = 2 a y = 1, x = -1 a y = -2, což odpovídá výsledkům slovní úlohy řešené pomocí krokování na pásu.