Šipkové grafy

Od metody pokus-omyl k lineární funkci.

Strukturální prostředí Šipkové grafy připomíná prostředí Hady. Nejčastěji jde o spojení dvou hadů se stejným začátkem i koncem. Začíná se v levém horním poli a ve směru šipek provádíme požadované početní operace.

Jedním ze záměrů prostředí je řešení kalkulativních úloh. Toto řešení ale má vyšší cíl než procvičení mechanického počítání, cílem je vyřešit rébus: šipkový graf. Děti takové počítání více baví, nepociťují jej jako nudu.

Didaktických cílů prostředí je více: objevení řešitelské strategie přes evidenci výsledků, zkušenosti s lineární funkcí a jejích vlastností, zkušenosti s řešením lineární rovnice nebo roznásobování závorek.

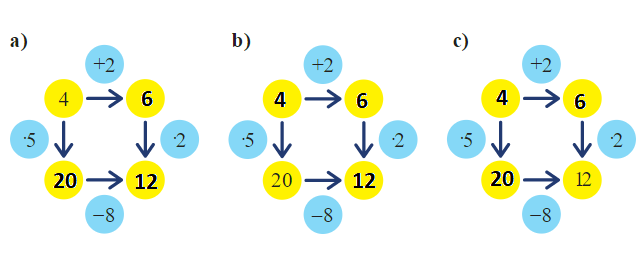
Úloha 1: Vyřeš šipkové grafy.

Ač se jedná ve všech třech případech o stejný šipkový graf, není jedno, jak úlohu zadáme. První úloha je nejjednodušší, žáci provádí výpočty: první cestou (4 + 2 = 6, 6 · 2 = 12), druhou cestou (4 · 5 = 20, 20 – 8 = 12). Druhá a třetí úloha jsou obtížnější, protože se v nich používají i inverzní operace (20 : 5 = 4 nebo 12 + 8 = 20).

Další úlohy jsou oproti předchozím obtížnější. Není již okamžitě vidět, jak nějaké z čísel doplnit. V začátcích žáci používají metodu pokus–omyl. Zkouší do levého horního rohu dosazovat čísla a z rozdílu výsledků obou cest levé horní číslo upravují.

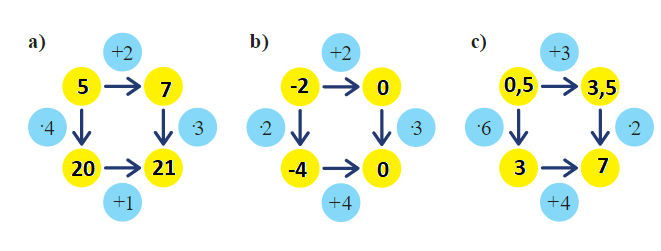
Úloha 2: Vyřeš šipkové grafy.

V první úloze žáci přirozeně vlevo nahoře zvolí 1. Jedna z cest má výsledek 5 (1 · 4 + 1). Druhá z cest 9 ((1 + 2) · 3). Rozdíl obou cest je 4. Zkusí číslo 2 a pozorování opakují.

Tím se postupně učí svou řešitelskou strategii vylepšovat a objevují zákonitosti a vztahy v rámci jedné cesty, i mezi oběma cestami – viz další úlohy.

Prostředí Šipkové grafy je dále rozvíjeno v 6. a 7. ročníku. Žáci pracují v oboru desetinných čísel, postupně opouštějí řešení metodou pokus–omyl a šipkové grafy řeší pomocí soustavy rovnic nebo pomocí jedné rovnice. Řeší také úlohy s parametrem (číslem, které může nabývat různých hodnot) a zabývají se problémem řešitelnosti šipkového grafu.

Úlohy se šipkovými grafy pomalu směřují k rovnicím. Pokud žáci spontánně rovnice nezačnou používat, lze jim dát pomocnou radu. Tou je dosazení proměnné x do levého horního pole. Není třeba spěchat a vždy by měli mít žáci dostatek času k tomu, aby dospěli k vlastnímu objevu.

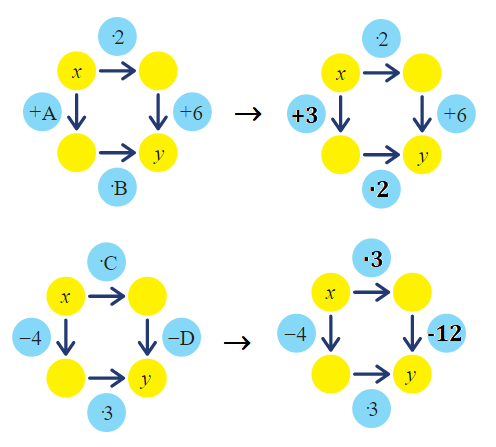
Úloha 3: Najděte čísla A, B, C, D tak, aby obě cesty začínající na vstupu x daly na výstupu y stejné číslo.

Šipkové grafy jsou strukturálním prostředím. To nám umožňuje dobře rozšiřovat číselný obor, ve kterém se pracuje.

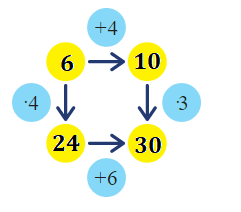
Úloha 4: Vyřešte šipkový graf.

Žáci zjišťují, že je dobré vést evidenci svých pokusů o vyřešení grafu. Výsledky zapisují do tabulky.

Jiná metoda spočívá v tom, že žáci označí číslo v levém horním rohu x a napíší rovnici: (x + 4) · 3 = x · 4 + 6, kterou vyřeší. Důležité je, aby žáci měli prostor k tomu využívat strategii podle svých potřeb.

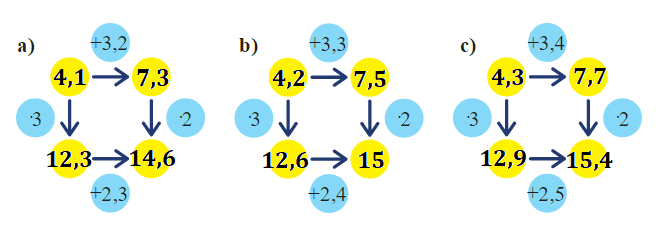
Úloha 5: Vyřešte šipkové grafy, víte-li, že levé horní číslo je větší než 4 a menší než 4,5.

V této úloze se pracuje s desetinnými čísly, v případě potřeby lze využít i zlomky.

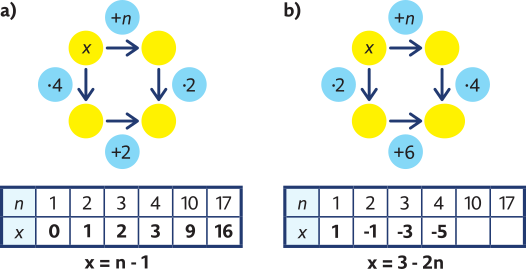
Úloha 6: Vyřešte šipkový graf pro všechna n uvedená v tabulce. Najděte vztah mezi čísly n a x.

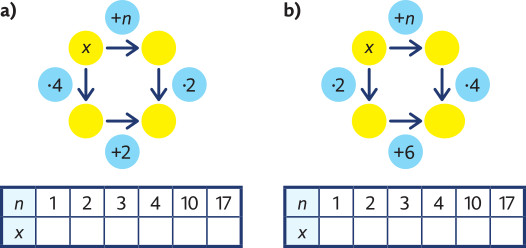
Úloha s parametrem může být pro žáky obtížná. Žáci mají několik možností, jak ji řešit: doplní tabulku a dívají se na závislost mezi x a n. U druhého grafu je obtížnější závislost najít, přesto se pravděpodobně najdou žáci, kterým se to podaří. Pokud se žákům úloha vyřešit nepodaří, nevadí, provedli spoustu výpočtů. Pokud se již dříve objevilo roznásobování závorek, zobecnění nebude problém, ale je důležité, aby s takovou myšlenkou přišli žáci sami.

Žáci se seznamují s důležitými vztahy lineární funkce. Jedním z nich je: Pokud známe dvě hodnoty lineárního výrazu, pak jsou známy hodnoty všechny.

Následující úloha má dva cíle. Prvním je žákovská tvorba úloh. Ta bývá pro žáky často těžkým oříškem, protože vyžaduje určitý nadhled a porozumění. Druhý cíl je diagnostický. V tomto případě lze z procesu tvorby šipkových grafů a), b) a c) zjišťovat úroveň porozumění lineárním rovnicím.

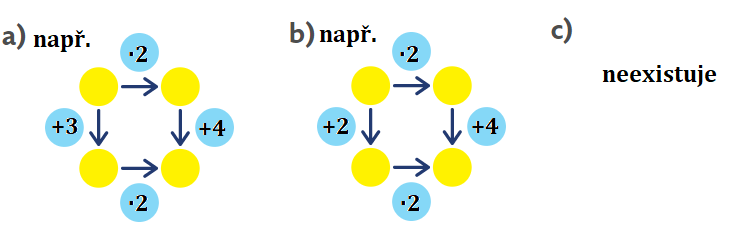
Úloha 7: Vymyslete šipkový graf, který
a) nemá řešení
b) má nekonečně mnoho řešení
c) má právě dvě řešení.