
Prostředí:

Prostředí:
Lineární rovnice a jejich úpravy v sémantickém kontextu.
Váhy jsou jedním ze základních nástrojů pro modelování lineárních rovnic. Při řešení úloh se rozvíjí zkušenosti s ekvivalentními úpravami rovnic a jejich soustav, tj. takovými úpravami, po kterých se řešení rovnice nezmění. Žáci získávají zkušenosti s roznásobováním závorek nebo myšlenkou substituce.
Je vhodné začít aktivitami, při kterých si děti vážení prakticky vyzkouší. K tomu lze použít např. klasické ramínko, na jehož konce lze zavěsit např. igelitové pytlíky. Do nich si mohou děti dávat různá závaží a pozorovat, co se s ramínkem děje. Váhy zavádíme na konci prvního stupně s výhledem na stupeň druhý.
Váhy jsou jedním ze základních nástrojů pro modelování lineárních rovnic. Váhy zavádíme na konci prvního stupně s výhledem na stupeň druhý.
Úloha 1: Kolik váží jedna kulička?
Na této jednoduché rovnici si žáci nejprve vyjasňují důležité pravidlo: V jedné rovnici stejné objekty mají stejnou hmotnost. Tím se předejde pozdějším možným nedorozuměním.
Některé děti úlohu řeší metodou pokus–omyl, některé objeví jednu z ekvivalentních úprav: Pokud obě strany rovnice vydělím nenulovým číslem, řešení rovnice se tím nezmění.
Kolik váží jedna kulička?
Pokud mají žáci zkušenosti s reálným vážením, mají větší šanci objevit další ekvivalentní úpravu.
Tu lze využít v této úloze: Pokud z obou stran rovnice odebereme stejné závaží, řešení rovnice se tím nezmění.
V tomto případě odebereme z obou stran 1 kg, dvě kuličky jsou 4 kg, proto jedna kulička váží 2 kg.
Takové zkušenosti přispívají v budoucnu k důležitému porozumění. Např. v rovnici 3x + 1 = 13 jsme nejednou slýchávali: Jedničku si převedeme na druhou stranu, takže to bude „minus“ a dostaneme rovnici 3x = 13 – 1. Bohužel, často děti toto pravidlo interpretují bez porozumění a nezřídka se jim poté plete s dalšími pravidly a poučkami. Věříme, že modelování na skutečných rovnoramenných vahách nebo podobných nástrojích (např. ramínkách) přispívá k lepšímu chápání těchto pravidel.
Úloha 2: Kolik váží jedna kulička?
Úloha 1:
V obou případech kulička váží 2 jednotky (kilogramy).
Úloha 2:
a) kulička = 6
b) kulička = 3
c) kulička = 5
d) kulička = 4
Na druhém stupni někteří žáci stále používají metodu pokus–omyl, někteří již používají jiné strategie (ekvivalentní úpravy, přepis do rovnic atd.).
Úloha 3: Zjistěte, jakou váhu (hmotnost) má krychle, koule
a váleček?
Úloha 4: Vyřešte.
Před řešením této úlohy si děti vyjasní, co obrázek znázorňuje.
V obou úlohách jsou na miskách vah umístěny balíčky, pod vahami je balíček rozbalen – děti vidí, co každý obsahuje. Některé trpělivě ) překreslují obsahy balíčků na misky vah, jiné už zápis zkracují, takže se objeví v úloze a) například zápis 10 + 2v = 5v + 1, případně i soustava rovnic „dva balíčky jsou 5 válců a jedna, jeden balíček je válec a pět,“ tedy 2b = 5v + 1, b = v + 5.
Se zápisem rovnice se děti setkaly už dříve, i na prvním stupni – například při řešení úloh z prostředí Mince.
Úloha 5: Rovnice znázorněte jako úlohu o vahách a vyřešte.
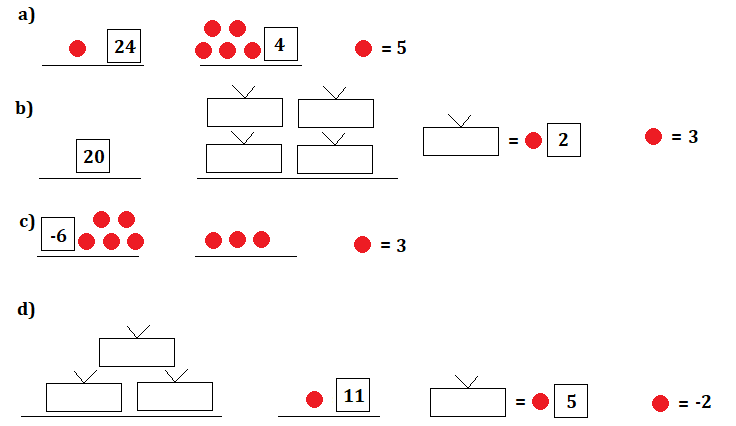
a) k + 24 = 5 · k + 4
b) 20 = 4 · (y + 2)
c) 5 · z – 6 = 3 · z
d) 3 · (5 + x) = x + 11
U úlohy b) se děti se setkávají se závorkou. Vždy se ve třídě ozve některé dítě se sdělením: „To je jako ten balíček.“
U úlohy c) vzniká obvykle diskuze o tom, jak znázornit číslo –6. Někteří žáci navrhují, že misku vah „nadlehčí“ (např. zavěšeným balónkem). Objevilo se i řešení, že žák navrhl, že „to číslo přesuneme na druhou stranu vah a bude kladné.“ Zapsal tedy rovnici 5 · z = 3 · z + 6, což mu ostatní odsouhlasili. Někteří žáci používají i závaží –6 s tím, že jim nepřekáží, že v životě taková věc možná není.
U úlohy d) žáci úlohu do vah překreslí snadno. Některé však zarazí výsledek –2. Je znovu vhodné nechat děti, ať si situaci vyjasní. Pokud žáci závaží –2 kg nepřijmou, je možné úlohu přeformulovat do jiného prostředí, např. Šipkové grafy, kde záporné řešení je běžné – viz další úloha.
Úloha 6: Přepište váhovou rovnici jako šipkový graf.
Úloha 7: Zjistěte váhu krychle a koule.
Úloha 8: Vyvažte krychli pomocí několika válců a libovolného závaží.
Hmotnost krychle označíme jako k, hmotnost válce v a hmotnost koule s. Zadání úlohy, kdy je třeba vyjádřit k pomocí několika v a čísla (to určuje počet kilogramů) směřuje už k úpravám algebraických výrazů.
Úloha 3:
a) krychle = 5
b) koule = 5
c) váleček = 1,25
Úloha 4:
a) válec = 3
b) koule = 4
Úloha 5:
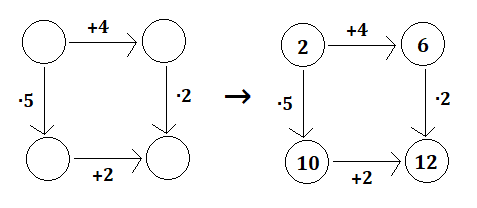
Úloha 6:
2 · (x + 4) = 5 · x + 2
Úloha 7:
a) 3 a 9.
„Místo koule dám na druhých vahách 3 krychle a už vím, že 5 krychlí váží 15 kg.“
b) 2,5 a 4,5.
„Místo každé koule jsem si tam představil krychli a 2 kila, protože koule je krychle a 2 kila; pak z každé misky odeberu 6 kg a jednu krychli.“
Je zde použita klíčová myšlenka používaná při úpravách rovnic: stejný objekt můžeme odstranit z obou stran při zachování rovnosti (aniž známe hmotnost objektu).
c) 3 a 7. Náročná úloha.
„Přidám na každou misku druhých vah krychli a pravé misce pak místo krychle a koule dám 10 kg; vím, že 3 krychle váží 21 kg.“
Úloha 8:
a) krychle = 2 válce + 0,5 kg
b) krychle = koule + 1 kg
To, že děti získaly dostatek zkušeností při řešení úloh v prostředí Váhy, jim posléze velmi napomáhá řešit soustavy rovnic. Kdy začnou používat výhradně písmena místo obrázků, záleží na individuálních možnostech jednotlivců. Jeden žák už v šestém ročníku přepsal váhovou rovnici na číselnou a správně ji vyřešil. Postupem času i ostatní žáci odhalují, že „ta váhová rovnice a ta s písmeny vyjadřují totéž“ (viz následující úloha) a s jejich úpravami nemívají těžkosti. Dosazovací i sčítací metoda řešení soustav rovnic jsou pro ně přirozené, často velmi snadné.
Úloha 9: Vyřešte.
Úloha 9:
a) + c) krychle (k) = 8, válec (v) = 4
b) + d) krychle (k) = 2, válec (v) = 3