Prostředí:
Vláčky
Nové prostředí Vláčky zavádíme hned v první třídě. Pracuje se v něm s barevnými hranolky. Znázorňují vagónky, jejichž skládáním získáváme vláčky.
Prostředí:
Nové prostředí Vláčky zavádíme hned v první třídě. Pracuje se v něm s barevnými hranolky inspirovanými tzv. Cuisenairovými hranolky (Cuisenaire rods). Jednotlivé barevné hranolky znázorňují vagónky, jejichž skládáním získáváme vláčky. Porovnáváním délek jednotlivých barevných hranolků se objevují vztahy, které jsou přehledně vidět v tabulce.
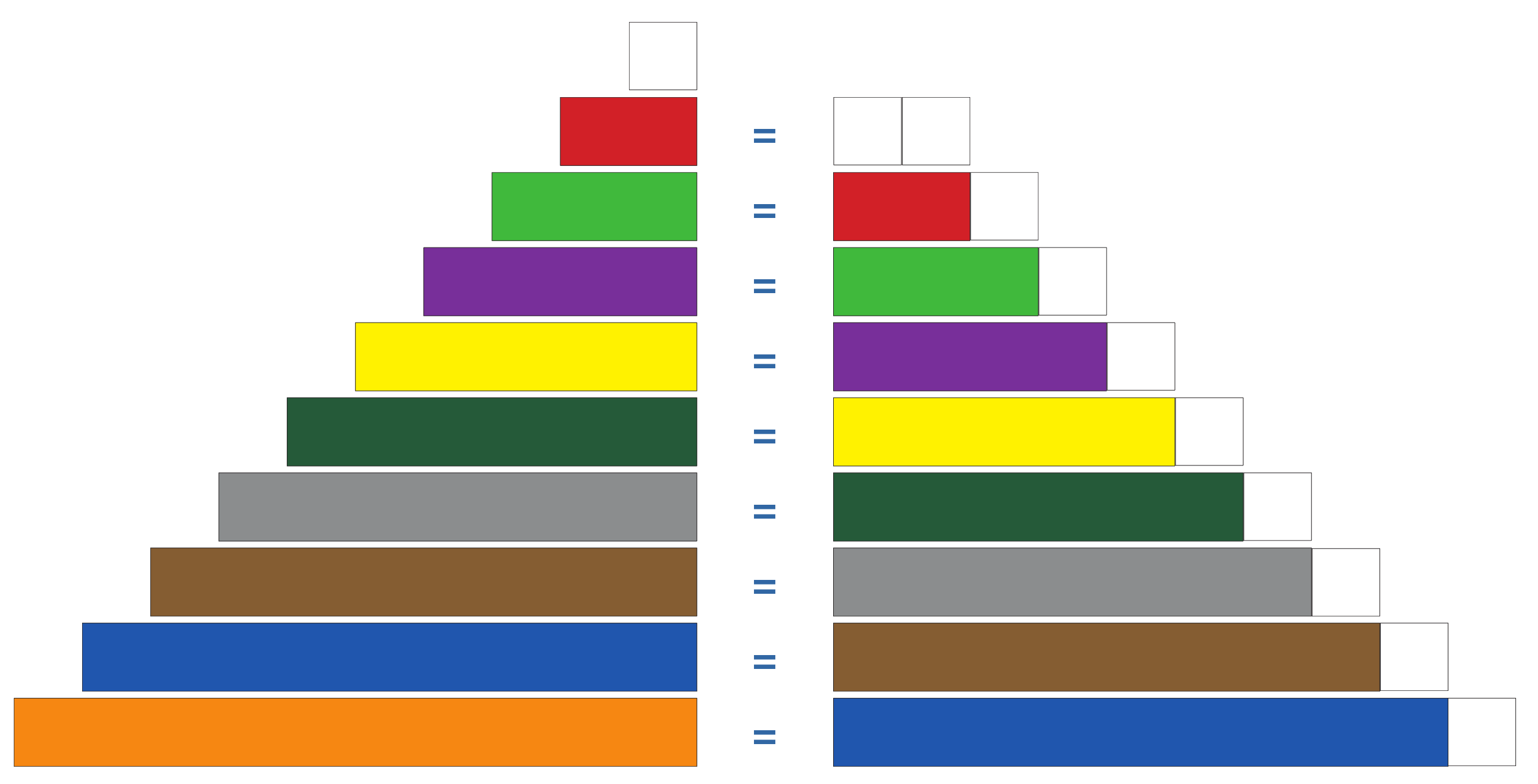
Není vhodné, aby dospělý tyto vztahy dítěti ukazoval, natož aby prozradil myšlenky o délkách vagónků (bílý = 1, červený = 2, zelený = 3 atd.). Tím by ochudil dítě o radost z objevování a úlohy by se staly pouhým počítáním s čísly. Navíc by děti přicházely o zkušenosti, které jim později umožní řešit mj. lineární rovnice.
Vláčky připomínají prostředí Dědy Lesoně, které vstupuje do učebnic ve druhé třídě. Podstatným rozdílem je to, že v prostředí Vláčky děti objevují vztahy pomocí porovnávání. V Dědovi Lesoňovi jsou tyto vztahy dány dohodou (síla 2 myší = síla 1 kočky). I proto platí, že Vláčky nedoporučujeme zavádět bez používání pomůcek (barevných hranolků nebo papírových náhražek) a že prostředí Vláčky (1. třída) má předcházet prostředí Děda Lesoň (2. třída).
Úloha 1: Z vagónků postav vláčky.
Barevné vagónky zavádíme postupně. V úvodní úloze se pracuje s vagónky bílými, červenými a zelenými. Důležité je, aby si děti s hranolky hrály, manipulovaly s nimi a porovnáváním zjišťovaly první vztahy: BB = Č, ČB = Z, BBB = Z. Objeví se i diskuze, zda může být vláček i jednovagónkový (doporučujeme, že ano) nebo zda vláček BČ je stejný jako vláček ČB? Tuto odpověď lze zcela nechat na dítěti. Většinou se děti přikloní k různosti vláčků („je přeci rozdíl, zda je červený vagónek první, nebo druhý”). Pokud vláčky budeme považovat za různé, přinese to větší počet řešení.
Úloha 2: Postav stejně dlouhé vláčky jako fialový vláček.
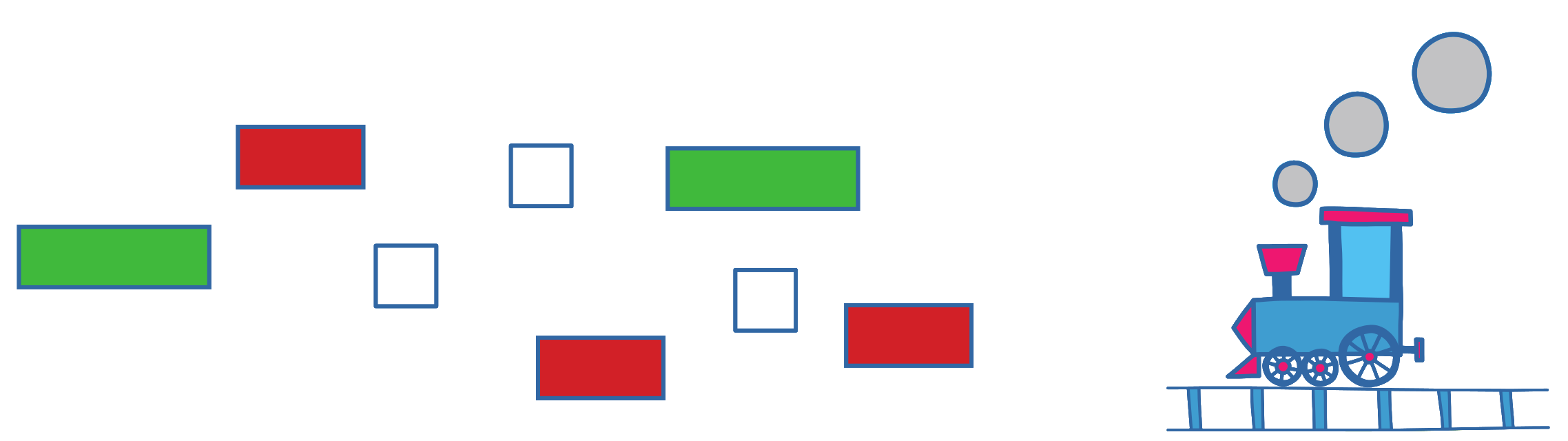
Další vagónky zavádíme tím způsobem, že z galerie vagónků sestavujeme vagónek nový – zde je nový fialový vagónek, který odpovídá 4 bílým vagónkům.
Úloha 3: Najdi vagónek stejně dlouhý jako jsou vláčky na obrázku.
Úloha 3 je otočena oproti úloze 2. V předchozích úlohách jsme k dlouhému vagónku hledali stejně dlouhé vláčky. Teď k dvouvagónkovému vláčku hledáme stejně dlouhý jednovagónkový vláček.
Úloha 4: Jaký vláček je delší? Zakroužkuj a doplň.
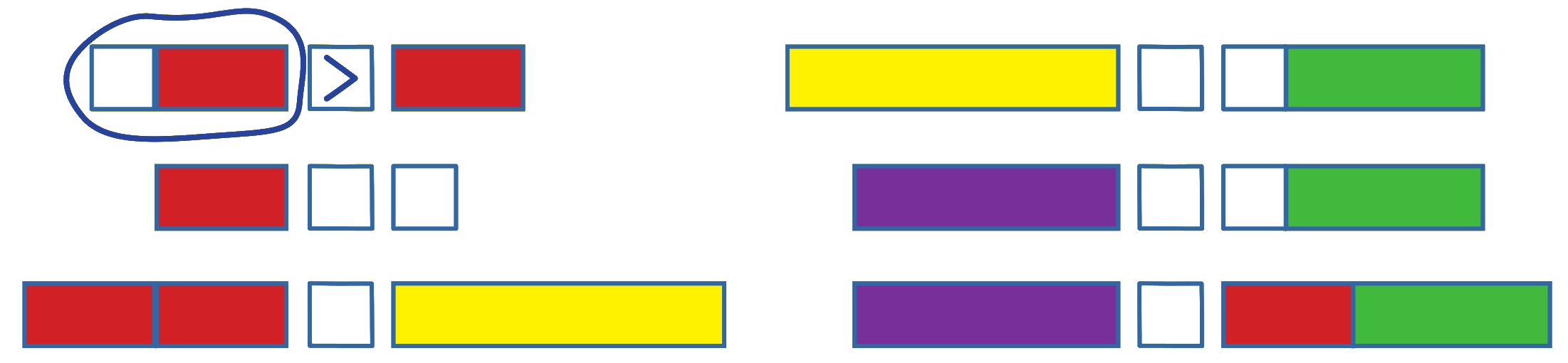
Úlohy s porovnáváním délky vláčků odpovídají úlohám v přetahování (které družstvo má větší sílu) u zvířátek Dědy Lesoně. Například první řešená úloha odpovídá úloze: myš + kočka > kočka. Není na učiteli nebo dospělém, aby tuto podobnost dítěti ukázal. Pokud s tím přijde dítě samo, je to v pořádku.
U úloh s nerovnostmi lze zadat další úlohu: Jaký vagónek musíme přidat ke kratšímu vláčku, aby vláčky byly stejně dlouhé?
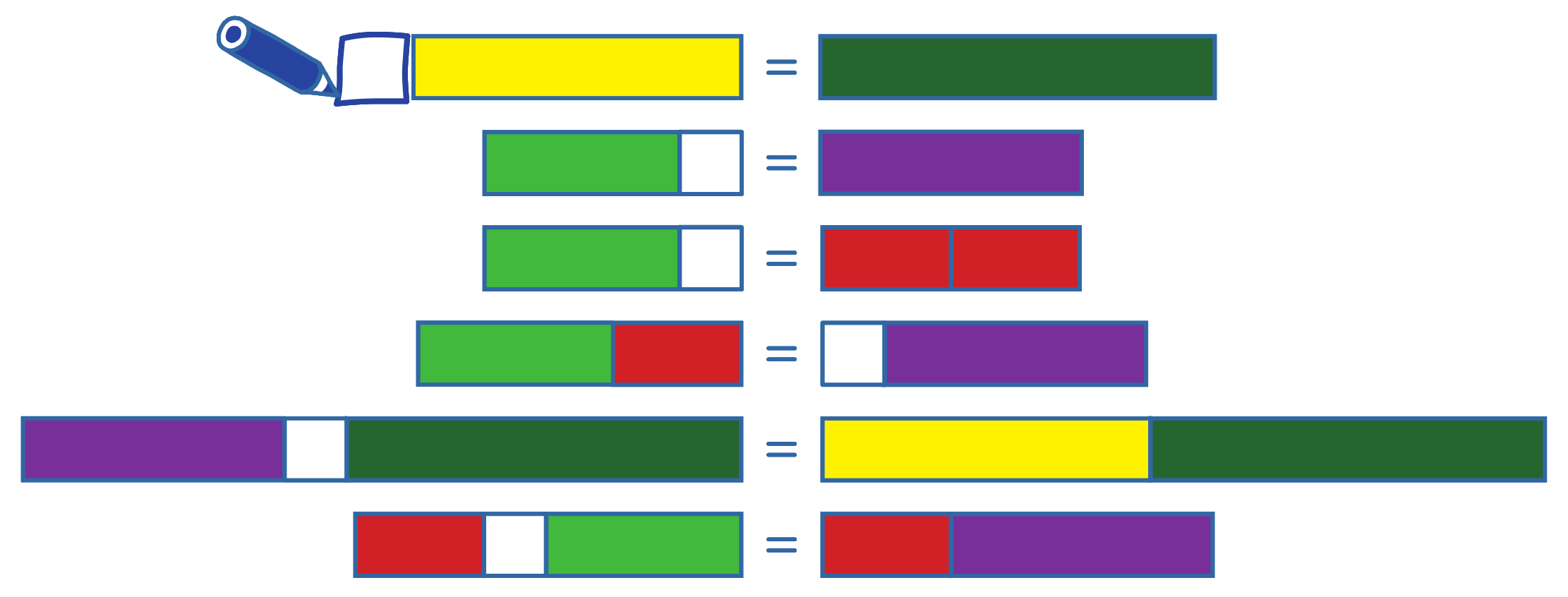
Úloha 5: Doplň jeden vagónek, aby vláčky byly stejně dlouhé.
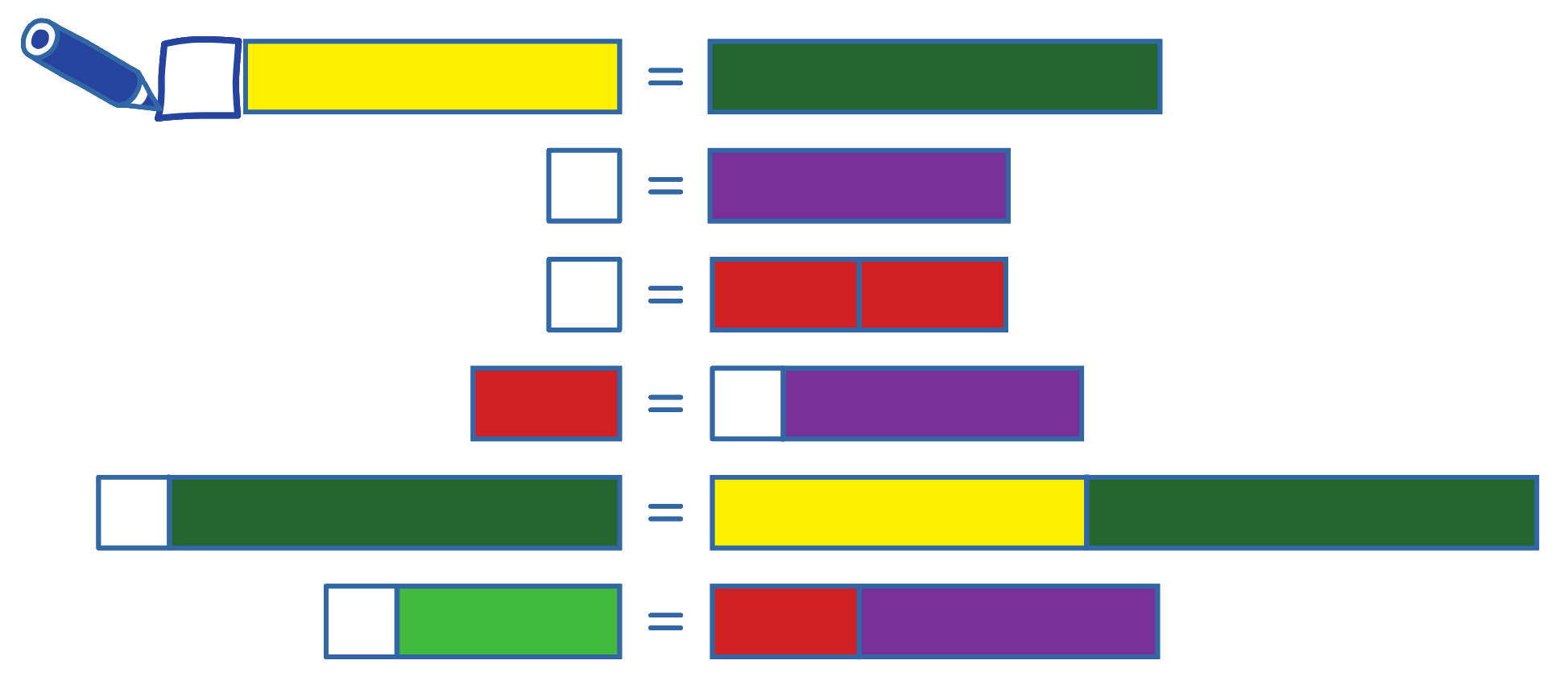
I následující úlohu lze převést do prostředí Dědy Lesoně. První řešená úloha by zněla: Jaké jedno zvířátko máme přidat ke koze tak, aby družstvo bylo stejně silné jako beran (v jazyku čísel ? + 5 = 6)? Výsledkem je myš (číselně 1).
Ve Vláčcích děti budou úlohu pravděpodobně řešit porovnáváním. Např. u druhé úlohy si postaví pod sebe bílý a fialový vagónek a zjistí, že k bílému musí doplnit zelený vagónek. Některé děti ale manipulaci potřebovat nebudou, ty mají do úlohy již lepší vhled. U páté úlohy někoho napadne, že lze tmavě zelené vagónky z obou stran odebrat a úloha se tím zjednoduší (? + B = Ž).
Takové úlohy (podpořené manipulací) přispívají k lepšímu porozumění ekvivalentním úpravám rovnic, tedy k poznání, že pokud odebereme z obou stran stejnou hodnotu, řešení rovnice se tím nezmění.
Úloha 6: Jaký vagónek je schovaný pod plachtou?
Nový typ úloh odpovídá úlohám s maskami v prostředí Děda Lesoň. V depu jsou zaparkované vagónky, které vidíme zepředu. Ty, které jsou schované pod plachtou, jsou označeny takto:
. Úkolem je vyřešit, jakou barvu má schovaný vagónek. V rámci jedné úlohy jsou vagónky stejné. Pokud bychom chtěli schovat více barevných vagónků a barvy odlišit, lze použít další masku, např.
.
Děti budou v začátcích řešit úlohu porovnáváním barevných hranolků. Později začnou používat matematickou myšlenku substituce (místo červeného vagónku si dají dva bílé), některé i objeví použití číslic. Je důležité, aby je v tomto dospělý coby autorita neovlivňoval.
Úloha 7: Najděte dva stejně dlouhé vláčky, z nichž jeden obsahuje jeden bílý vagónek a pak jen již samé zelené vagónky, druhý vláček obsahuje pouze vagónky fialové.
V řeči čísel a písmen můžeme rovnici napsat ve tvaru 1 + 3x = 4y (kde x je počet zelených a y počet fialových vagónků). Do budoucna tím získávají zkušenosti s tzv. diofantovskou rovnicí, nicméně v 1. třídě je taková úloha pro děti neřešitelná. V kontextu vláčků ji ale dovedou dobře řešit.
Úloha 2:
Celkem je tedy 7 řešení.
Úloha 3:
Úloha 4: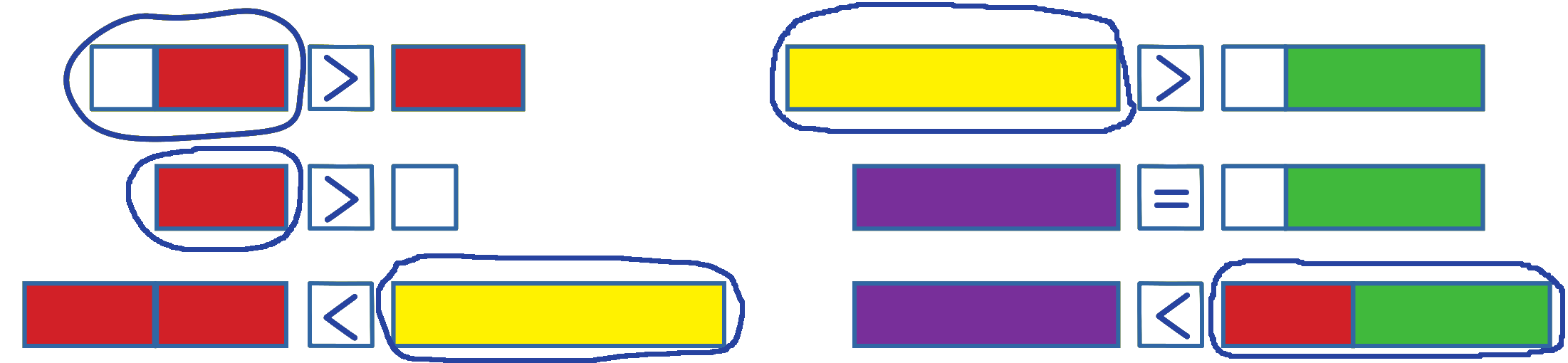
Úloha 5:
Úloha 6:
Pozor na světle a tmavě zelené.
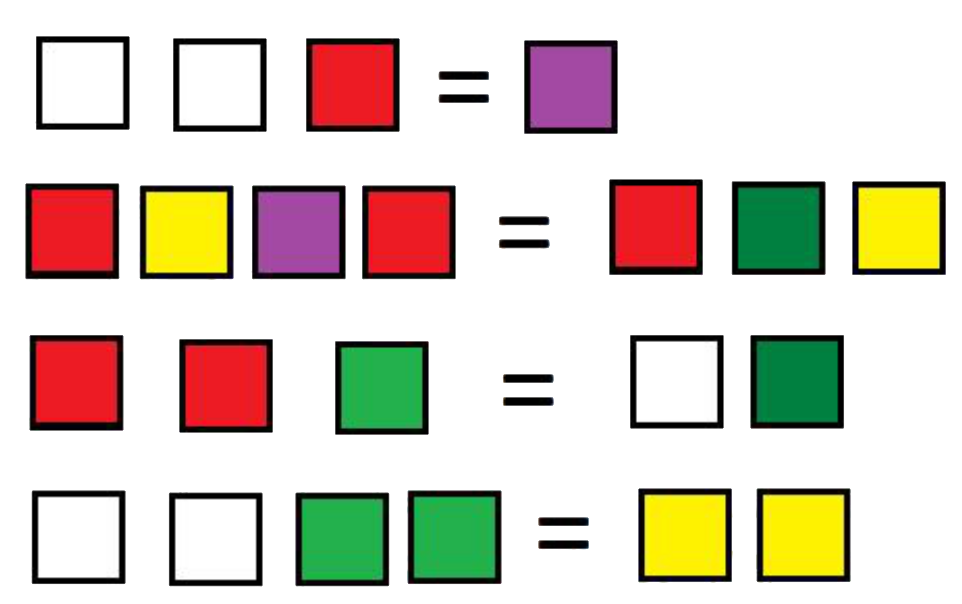
Stejně jako v prostředí Děda Lesoň se může objevit i zde přepis do čísel a do rovnic. Pro některé žáky tato desémantizace může být urychlením, pro některé to ale vede ke ztrátě představ. Dospělý, který takové zjednodušení dětem nabídne, předpokládá, že tím urychlí porozumění dítěte celému prostředí. Neuvědomuje si, že některé děti tím přejdou od porozumění k paměťovému učení a k formálním poznatkům.
Proč může být pro mladší děti přepis do čísel nevhodný, ukazuje také následující úloha.
Úloha 7:
1 zelený a 1 fialový, 5 zelených a 4 fialové, 9 zelených a 7 fialových atd.
Obecně by šlo zapsat řešení jako: (1 + 4k, 1 + 3k), kde k je 0, 1, 2, ...
Výraz 1 + 4k udává počet zelených vagónků, 1 + 3k počet vagónků fialových.
V modrých učebnicích prof. Hejného a kol. H-mat, o.p.s. pro 1. ročník vydávaných v tomto roce přímo v H-mat, o.p.s. najdete nové prostředí: Vláčky. O tomto prostředí si můžete přečíst více zde na blog...
