Zlomky

Utváříme představu o zlomku od části celku k číslu 

Zlomky znali již staří Babyloňané. Více než tisíc let poznávali jen zlomky kmenové, tj. 1/2 , 1/3 , 1/4 , …*
Proto i my s těmito zlomky seznamujeme děti již od první třídy.

* Z typografických důvodů používáme pro zápis zlomků šikmé lomítko. Děti se však setkávají v našich učebnicích se standardním zápisem zlomku: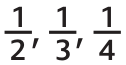

I dítě předškolního věku běžně slyší, že maminka kupuje půlku chleba, že pojedeme čtvrt hodiny, že skončila první třetina zápasu. Hlubší porozumění těmto slovům dítě získá, když samo dělí lentilky nebo koláč mezi dva nebo i více kamarádů.

Lentilky dělí rozdělováním „jedna tobě, jedna mně, jedna tobě,…“. Když je lentilek lichý počet, dostane kamarád o jednu více. Zjistíme to, když lentilky seřadíme do dvou zástupů vedle sebe.

Koláč dělí dítě krájením. Jedno dítě krájí a druhé si jako první volí svoji polovinu. I dělení koláče na čtvrtiny umí více předškoláků. S dělením koláče na třetiny je to složitější.

Zeptá-li se dítě rodiče, co je to pětina, řekneme mu, že když koláč spravedlivě rozdělíme mezi pět dětí, každý dostane jednu pětinu. Když se předškolák neptá, nic mu o zlomcích neříkáme, ani jej na tento jev neupozorňujeme. Snaha o předčasné vyučování dítěte může v jeho mysli vyvolat nechuť, ne-li odpor ke zlomkům.

Slova „rozpůlit“ a „polovina“ jsou vstupní branou do světa zlomků. Najít střed proužku papíru je totéž, co rozdělit proužek na poloviny.

Každý žák dostane proužek papíru a tužkou na něm vyznačí střed. Pak přeložením proužku zjistí, jak se mýlil. Úlohu mnoho žáků chápe jako výzvu naučit se najít střed. Ve svém vědomí tak propojují polovinu a střed, aritmetiku a geometrii.

Úloha o dělení zvířátek do tří stejně silných družstev dává žákům zkušenost se zlomkem třetina, o čtvrtině se mluví v souvislosti s hodinami, na konci druhého ročníku žák zjišťuje, kolik dní je pětina června a kolik šestina června.

Na začátku třetího ročníku můžeme dětem nabídnout následující úlohy. Děti pracují se zlomky, pojmenovávají je, ale ještě nezapisují. Dříve se učí jim porozumět a pak až zapisovat.

Úloha 1: Polovina tyče je natřena na modro, čtvrtina na zeleno a zbytek na červeno. Jak dlouhá je modrá a jak červená část, když celá tyč měří a) 20, b) 60, c) 72 centimetrů?

Důležité zde je, že se děti seznamují s polovinou a čtvrtinou na jiném modelu, než jsou lentilky nebo pizza. Na obrázku vnímají, že dvě čtvrtiny jsou jako polovina. Když dáme dětem tyč nebo její obrázek, můžeme pracovat i s její skutečnou délkou a řešení mohou děti zjistit, nebo ověřit měřením.

Úloha 2: Čtvrtina tyče je natřena na modro, zbytek na zeleno. Jak dlouhá je modrá část a jak celá tyč, když zelená část měří a) 30, b) 60, c) 45, d) 21, e) 42, f) 63 centimetrů?

V zadání úlohy se mluví jen o čtvrtině, ale žák pracuje se zelenou částí, což jsou tři čtvrtiny. Tedy známe délku tří čtvrtin. Když si dítě nakreslí obrázek tyče a vyznačí čtvrtiny, jednu z nich obarví na modro, uvidí, že zelená část má tři čtvrtiny, tedy danou délku rozdělí na tři stejné části, a tak dostává čtvrtinu.

Ve čtvrtém ročníku začínáme zlomky zapisovat čísly. Žáci řeší i úlohy, které řešili písaři starého Egypta. Ti uměli zapisovat jenom kmenové zlomky a například zlomek 2/3 nevnímali jako část celku, ale jako jeden díl při dělení dvou chlebů mezi tři podílníky. Chleby dělili tak, že každý dostal úplně stejné kusy, těch kusů bylo co nejméně a byly různé. Nikdo neměl dva kusy stejné. Na obrázku vidíme, jak to dělali.

Tedy každý podílník dostává 1/2 + 1/6 chleba. Žáci řešením úlohy odhalí rovnost 2/3 = 1/2 + 1/6.Podobně, když dělí 3 chleby mezi 5 podílníků, nebo 2 chleby mezi 5 podílníků, odhalí žáci rovnosti 3/5 = 1/2 + 1/10 a 1/3 + 1/15.

Žáci se takto naučí rozkládat zlomky na součet kmenových zlomků. Sčítání a odčítání zlomků odhalí pomocí čokolády.

Úloha 3: Pomocí čokolády vypočítej a) 1/3 + 1/4 , b) 1/3 – 1/4

Čokoláda obsahuje 12 . 1/3 čokolády je jeden řádek, tedy 4 . 1/4 čokolády je jeden sloupeček, tedy 3 .
4 + 3 = 7 . Ale 1 = 1/12 čokolády.
Tedy a) 1/3 + 1/4 = 7/12 ; b) 1/3 – 1/4 = 1/12 .

Úloha 4: Čtverec na obrázku je rozdělen na 4 části. Obvod žlutého čtverce je 8 cm, obvod zeleného čtverce je 4 cm. Zjisti, jakou částí obsahu celého čtverce je a) zelený čtverec, b) obdélník složený z modrého a zeleného pole, c) žlutý čtverec, d) modrý obdélník.

Žák si může obrázek překreslit na čtverečkovaný papír. Ví, že strana žlutého čtverce je 2 a zeleného 1. Nakreslí tedy čtverec 3 × 3 a rozdělí jej stejně jako na obrázku. Zbytek je již jednoduchý.

Úloha 5: Podobný obrázek jako je ten z úlohy 4, ale rozměry má jiné. Víme, že obvod růžového obdélníku je 16 cm a obvod obdélníku složeného z modrého obdélníku a zeleného čtverce je 20 cm. Dále víme, že obsah žlutého čtverce je 9/16 obsahu celého čtverce. Zjistěte, jakou částí celého čtverce je modrý obdélník.

Žák může použít metodu pokus-omyl. Protože růžový obdélník má obvod 16 cm, jsou jeho rozměry 1 × 7, nebo 2 × 6, nebo 3 × 5. Budeme tedy vyšetřovat tři uvedené případy.

V pátém ročníku ke sčítání zlomů používáme i ciferník.

Úloha 6: Vypočítej pomocí ciferníku a) 1/2 + 1/6 , b) 2/5 + 1/2

Zlomek je nástroj na práci s částmi. Není to nástroj jediný. Druhý takový nástroj jsou desetinná čísla. To, že 1/2 = 0,5 a 3/4 = 0,75, znají již čtvrťáci. Teď přichází náročnější úlohy na propojení zlomků a desetinných čísel.

Úloha 7: Na číselné ose vyznač čísla 0, 1, 1/2, 1/3, 2/3, 1/6 a 5/6 . Zjisti, do kterého z intervalů tvého obrázku padne číslo: a) 0,1; b) 0,2; c) 0,3; d) 0,4; e) 0,5; f) 0,6; g) 0,7; h) 0,8; i) 0,9; j) 0,33; k) 0,34.