Většina rodičů současných žáků si asi pamatuje hry, které jsme hrávali na prvních počítačích. Pamatujete si na Tetris? Hra, kde nám z horní lišty “padaly” různé bloky sestavené z jednoho až šesti čtverečků. Ty jsme pak otáčeli a rovnali do řad, které po naplnění zmizely.
I když jsme si to neuvědomovali, jenom jsme si “hráli”, zdokonalovali jsme se ve vnímání tvarů, v počtu, zakládala se představa obsahu, otáčením se zdokonalovala orientace na ploše a v prostoru. Hra nebyla zařazena mezi didaktické pomůcky. Ale spoustě lidí pomohla při vytváření geometrických představ. To se žákům hodí do hodin matematiky, ale především se to hodí lidem v životě.
Geometrické a matematické představy jsou v matematice často úzce propojené - výsledek násobilky si můžete představit jako počítání obsahu obdélníků, nebo při rýsování si můžete vypomoct dopočítáním úhlů. Já sama jsem byla typ, že jsem si raději dopočítala nutné údaje, než bych je konstruovala. Ale když jsem viděla, jak někteří žáci řeší úlohy, na které bych já vytáhla aritmetiku, jenom geometrickým “citem” (oni to prostě “viděli”), tak jsem začala uvažovat, jak bych si svoje “vidění” geometrie mohla nějak zlepšit. Matemága asi již všichni znáte, ten má ale i jiné cíle. Chci se s vámi podělit o hry, které mi pomohly v zlepšování geometrických dovedností.
Jednou večer jsem narazila na hru Pythagorea. Začala jsem řešit jednoduché úlohy ve čtvercové mříži. Zjistila jsem, že mi dost pomáhají “triky”, které objevují žáci na 1. stupni při řešení úloh v mříži. Zkuste si třeba udělat kolmici ke každé z následujících úseček:
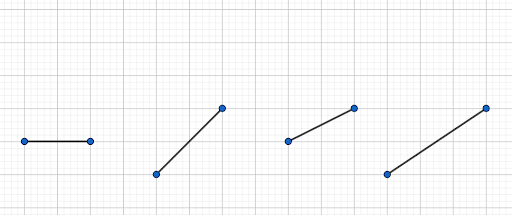
Hru Pythagorea jsem hrála intenzivně pár týdnů. Jednou jsem se zasekla na určité úloze a neuměla jsem se pohnout dál. Většinu věcí jsem měla hotovou, tak jsem hraní odložila s tím, že řešení nechám dozrát. Mezitím jsem se více věnovala tématu osnova přímek, které je v učebnici matematiky Hejného metodou, díl C. Po návratu ke hře Pythagorea jsem nástroj osnovy přímek použila a úloha šla relativně lehce vyřešit. A další úlohy taky. A celkově jsem zjistila, že moje vnímání geometrie se velmi zlepšilo.
Hra je postavená tak, aby hráče bavila a měli motivaci hrát dál (a tím se učit více a více). Začíná se od nejjednodušších úloh, které se postupně stávají těžší a těžší. Časem začnou být skutečně těžké. Je možné si najít výsledek, ale kdo někdy zažil pocit úspěchu z dobře vyřešené úlohy, málokdy hledá tyhle zkratky. A pokud poctivě vyřešíte úlohy v jednotlivých tématech, většinou získáte potřebné dovednosti pro řešení těžších úloh.
Každá úloha ve hře je zadána na stejném hracím plánu (čtvercová mříž velikosti 6x6 čtverečků) a používá stejné nástroje pro řešení (je zajímavé, jak silným nástrojem je přímka v čtvercové mříži). Tady je příklad vyřešené úlohy a příklad zadání:
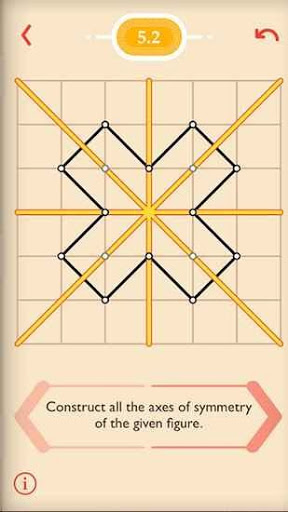
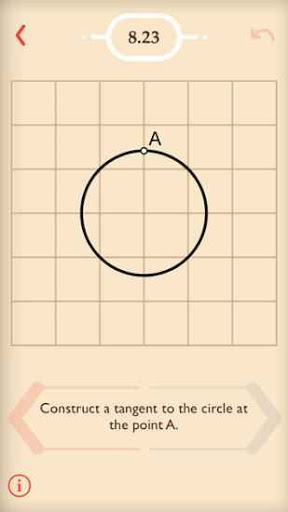
Ve výstavbě hry vidím podobnost s některými klíčovými principy Hejného metody:
- “Budování schémat” a “Práce v prostředích” - prostředí hry je neměnné, buduje se schéma čtvercové mříže. Všechny úlohy jsou zadávány podobným stylem. Když objevím nějaký princip v jednodušší úloze, můžu ho v těžší úloze použít.
- “Skutečná motivace” a “Radost z matematiky” - úkol, který chci vyřešit, mě láká. A když ho vyřeším, mám radost. Radost je tím větší, čím větší úsilí mě řešení stálo.
- “Přiměřené výzvy” - začíná se s lehkými úlohami, které pomáhají pochopit, jak hra funguje. Pak jsou úlohy těžší. Ale jsou postaveny tak, aby jednodušší úloha napomáhala řešení té těžší. A pokud nejsou lehčí úlohy (v daném tématu) vyřešené, hra vás k těžší úloze nepustí.
Hra Pythagorea (i další dále jmenované) je jenom v angličtině. Pro část dětí to není problém, ale pro některé ano. Ale pokud jim někdo na začátku pomůže, měly by se rychle zorientovat. Zadání je většinou jedna věta, která začíná slovem “Spoj” nebo “Sestroj” a pak je tam soubor matematických výrazů jako rovnoběžka, kolmice, trojúhelník, čtyřúhelník, rameno, základna trojúhelníku, … Na internetu se dá rychle najít překlad i vysvětlení použitých pojmů.
Po hře Pythagorea jsem objevila další hry:
- Pythagorea 60°- hra Pythagorea, kde hracím polem je mříž rovnostranných trojúhelníků.
- Euklidea - geometrické zadání úloh na čistý papír. K dispozici je přímka a kružítko. Pokud řešitel pomocí těchto základních nástrojů sestrojí další nástroj (třeba kolmici), může ho používat. Hra hodnotí nejen nalezení řešení, ale i počet úkonů, které hráč provedl. A pak nalezení všech řešení. Pro řešení vyšších levelů jsou potřeba určité znalosti ze SŠ.
- XSection - hra pracující s 3D objekty. Úkolem je sestrojit řezy různými tělesy, většinou různo-bokými hranoly nebo jehlany. Hra nevyžaduje žádné speciální znalosti, všechno potřebné je vysvětleno pomocí názorných obrázků. Ale i tak je řešení dost náročné (aspoň já jsem se musela často zamyslet).



Určitě existuje spousta dalších krásných her, které pomáhají rozvíjet geometrické představy. Vybrala jsem ty, které jsem sama hrála a přišly mi zajímavé a zároveň velmi užitečné. Více informací můžete získat třeba tady: https://www.facebook.com/Euclidea/ a pokud máte další tipy, můžete napsat níže do komentářů a podělit se tak s ostatními čtenáři o svoje tipy a zkušenosti.


Komentáře